Optimal Partial Graph Matching
Paper and Code
Oct 23, 2024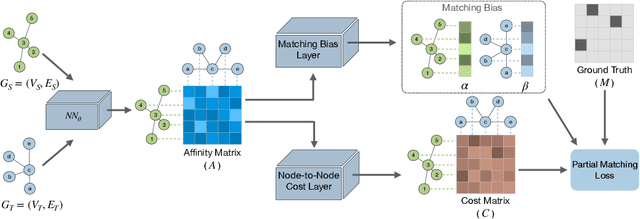
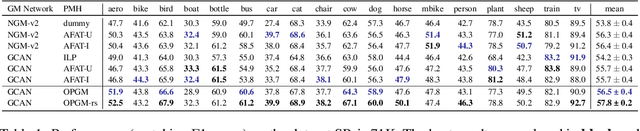
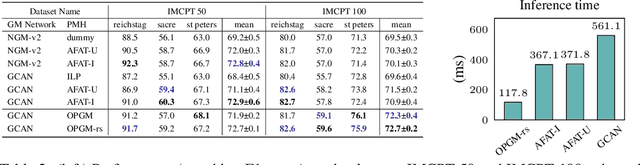
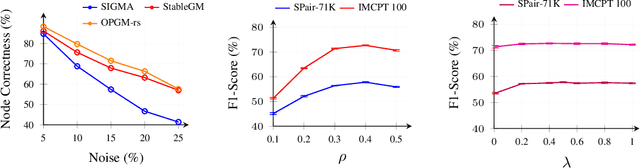
Partial graph matching addresses the limitations of traditional graph matching by allowing some nodes to remain unmatched, making it applicable to more complex scenarios. However, this flexibility introduces additional complexity, as both the subset of nodes to match and the optimal mapping must be determined. While recent studies have explored deep learning techniques for partial graph matching, a significant limitation remains: the absence of an optimization objective that fully captures the problem's intrinsic nature while enabling efficient solutions. In this paper, we propose a novel optimization framework for partial graph matching, inspired by optimal partial transport. Our approach formulates an objective that enables partial assignments while incorporating matching biases, using weighted total variation as the divergence function to guarantee optimal partial assignments. We employ the Hungarian algorithm to achieve efficient, exact solutions with cubic time complexity. Our contributions are threefold: (i) we introduce a robust optimization objective that balances matched and unmatched nodes; (ii) we establish a connection between partial graph matching and the linear sum assignment problem, enabling efficient solutions; (iii) we propose a deep graph matching architecture with a novel partial matching loss, providing an end-to-end solution. The empirical evaluations on standard graph matching benchmarks demonstrate the efficacy of the proposed approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge