Bayesian Regression Markets

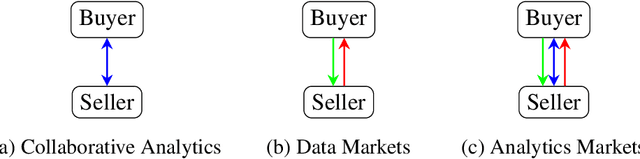
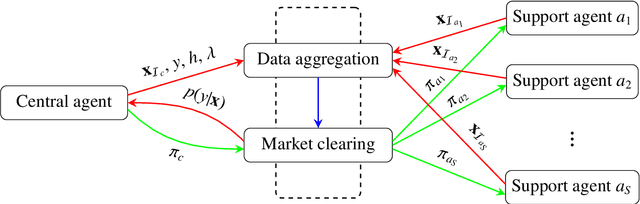
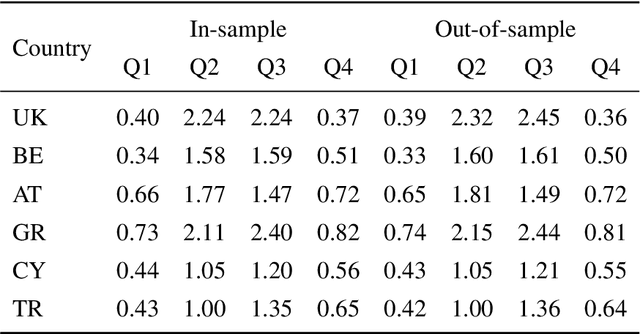
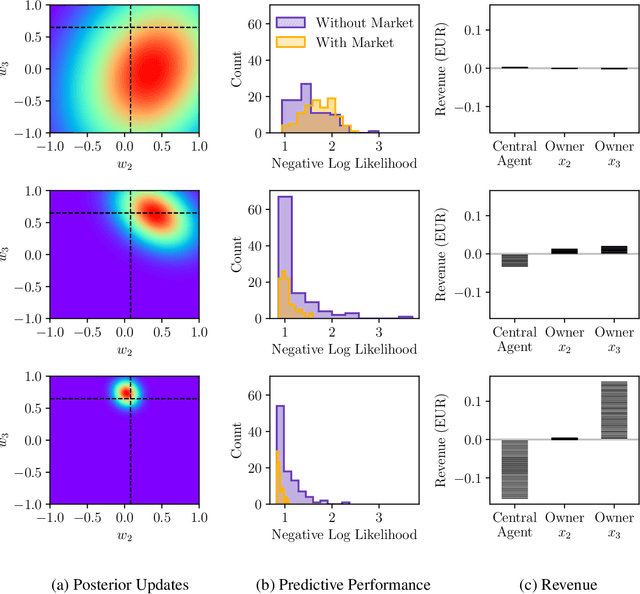
Machine learning tasks are vulnerable to the quality of data used as input. Yet, it is often challenging for firms to obtain adequate datasets, with them being naturally distributed amongst owners, that in practice, may be competitors in a downstream market and reluctant to share information. Focusing on supervised learning for regression tasks, we develop a \textit{regression market} to provide a monetary incentive for data sharing. Our proposed mechanism adopts a Bayesian framework, allowing us to consider a more general class of regression tasks. We present a thorough exploration of the market properties, and show that similar proposals in current literature expose the market agents to sizeable financial risks, which can be mitigated in our probabilistic setting.

Unit Commitment Predictor With a Performance Guarantee: A Support Vector Machine Classifier

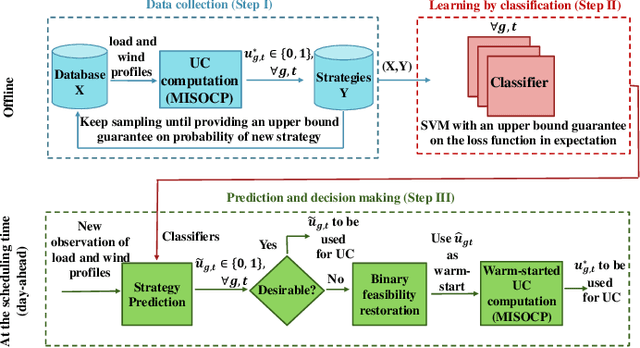
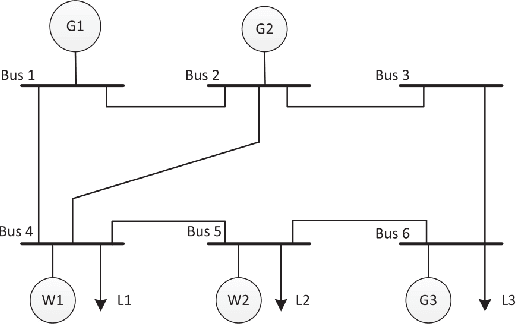
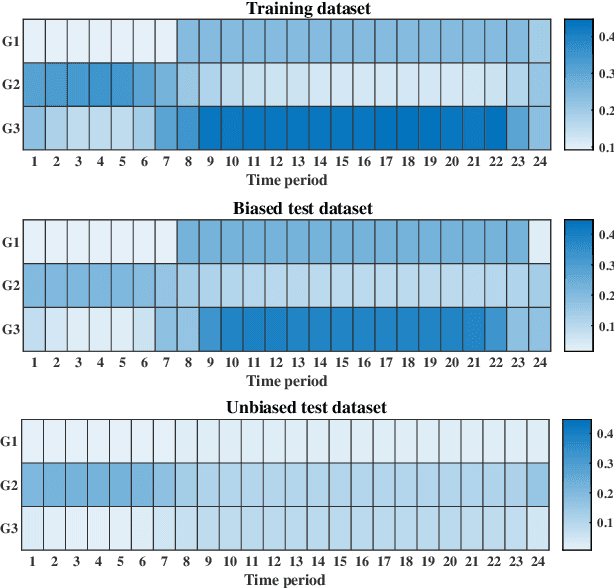
The system operators usually need to solve large-scale unit commitment problems within limited time frame for computation. This paper provides a pragmatic solution, showing how by learning and predicting the on/off commitment decisions of conventional units, there is a potential for system operators to warm start their solver and speed up their computation significantly. For the prediction, we train linear and kernelized support vector machine classifiers, providing an out-of-sample performance guarantee if properly regularized, converting to distributionally robust classifiers. For the unit commitment problem, we solve a mixed-integer second-order cone problem. Our results based on the IEEE 6-bus and 118-bus test systems show that the kernelized SVM with proper regularization outperforms other classifiers, reducing the computational time by a factor of 1.7. In addition, if there is a tight computational limit, while the unit commitment problem without warm start is far away from the optimal solution, its warmly started version can be solved to optimality within the time limit.

Online Decision Making for Trading Wind Energy

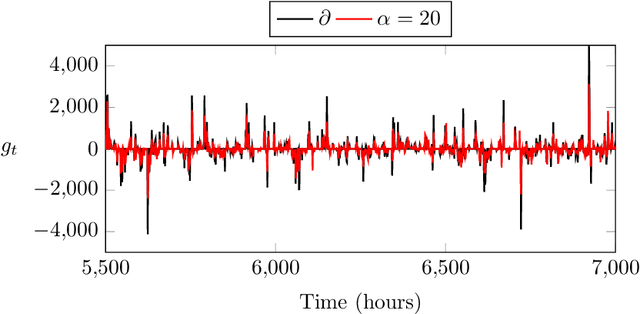
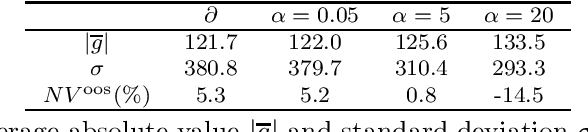
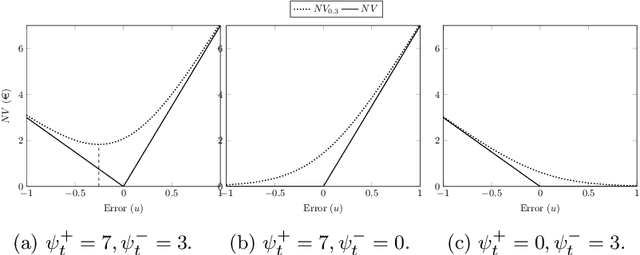
This paper proposes and develops a new algorithm for trading wind energy in electricity markets, within an online learning and optimization framework. In particular, we combine a component-wise adaptive variant of the gradient descent algorithm with recent advances in the feature-driven newsvendor model. This results in an online offering approach capable of leveraging data-rich environments, while adapting to non-stationary characteristics of energy generation and electricity markets, and with a minimal computational burden. The performance of our approach is analyzed based on several numerical experiments, showing both better adaptability to non-stationary uncertain parameters and significant economic gains.

Differentially Private Convex Optimization with Feasibility Guarantees

This paper develops a novel differentially private framework to solve convex optimization problems with sensitive optimization data and complex physical or operational constraints. Unlike standard noise-additive algorithms, that act primarily on the problem data, objective or solution, and disregard the problem constraints, this framework requires the optimization variables to be a function of the noise and exploits a chance-constrained problem reformulation with formal feasibility guarantees. The noise is calibrated to provide differential privacy for identity and linear queries on the optimization solution. For many applications, including resource allocation problems, the proposed framework provides a trade-off between the expected optimality loss and the variance of optimization results.