Bayesian Regression Markets

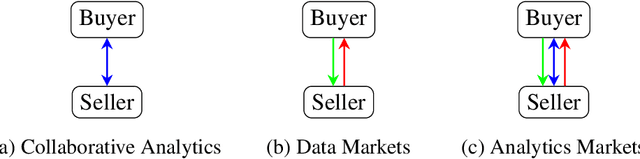
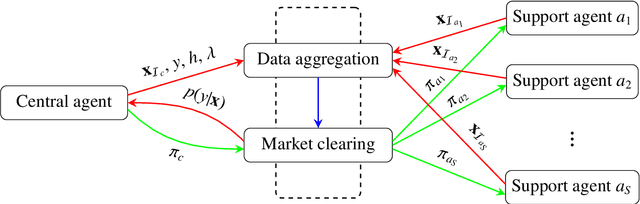
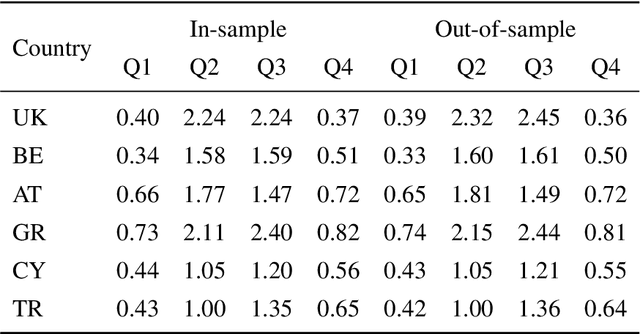
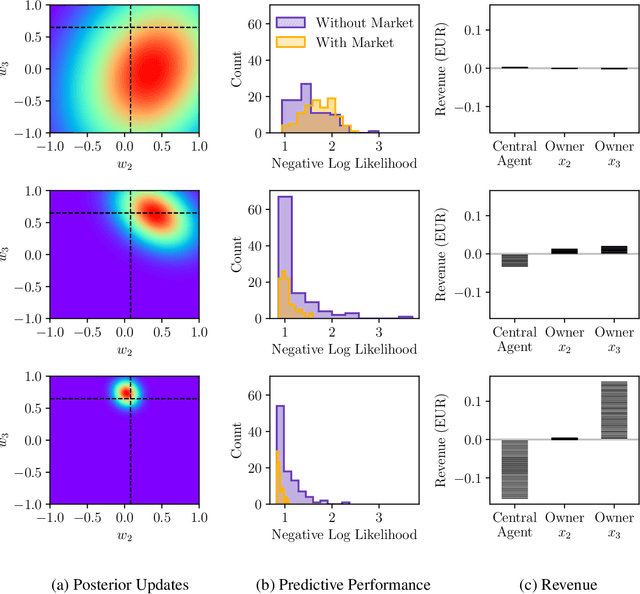
Machine learning tasks are vulnerable to the quality of data used as input. Yet, it is often challenging for firms to obtain adequate datasets, with them being naturally distributed amongst owners, that in practice, may be competitors in a downstream market and reluctant to share information. Focusing on supervised learning for regression tasks, we develop a \textit{regression market} to provide a monetary incentive for data sharing. Our proposed mechanism adopts a Bayesian framework, allowing us to consider a more general class of regression tasks. We present a thorough exploration of the market properties, and show that similar proposals in current literature expose the market agents to sizeable financial risks, which can be mitigated in our probabilistic setting.

Leveraging power grid topology in machine learning assisted optimal power flow

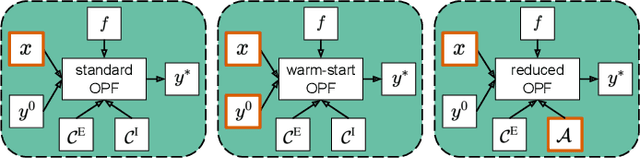
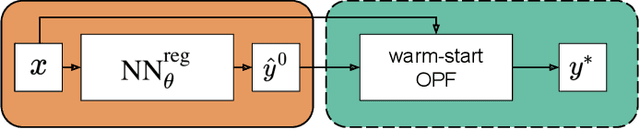
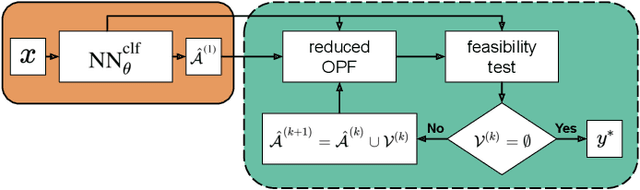
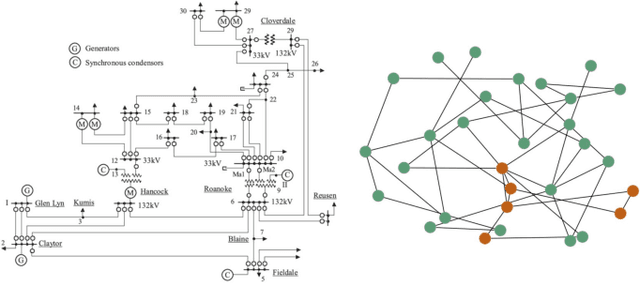
Machine learning assisted optimal power flow (OPF) aims to reduce the computational complexity of these non-linear and non-convex constrained optimisation problems by consigning expensive (online) optimisation to offline training. The majority of work in this area typically employs fully-connected neural networks (FCNN). However, recently convolutional (CNN) and graph (GNN) neural networks have been also investigated, in effort to exploit topological information within the power grid. Although promising results have been obtained, there lacks a systematic comparison between these architectures throughout literature. Accordingly, we assess the performance of a variety of FCNN, CNN and GNN models for two fundamental approaches to machine learning assisted OPF: regression (predicting optimal generator set-points) and classification (predicting the active set of constraints). For several synthetic grids with interconnected utilities, we show that locality properties between feature and target variables are scarce, hence find limited merit of harnessing topological information in NN models for this set of problems.

Deep learning architectures for inference of AC-OPF solutions

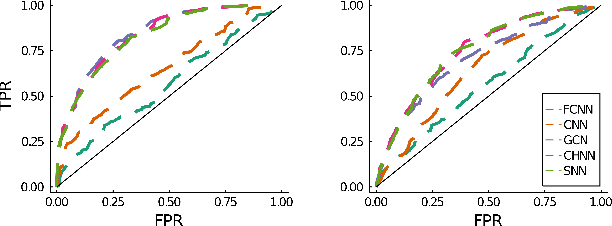
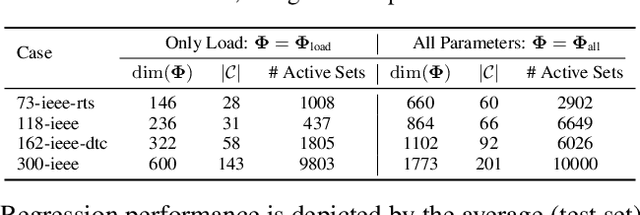
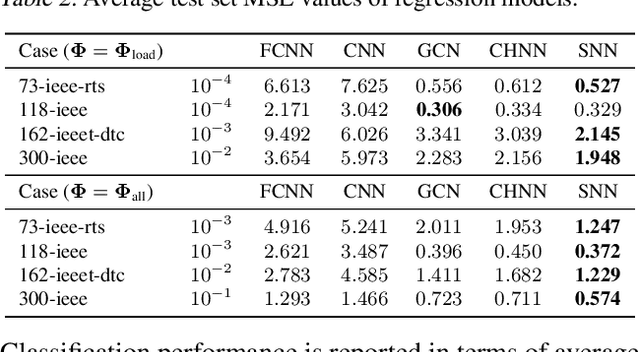
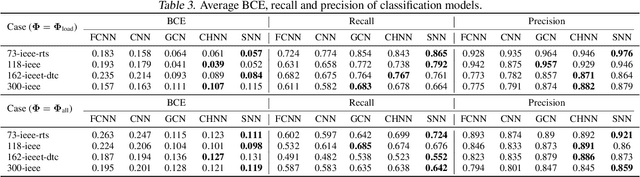
We present a systematic comparison between neural network (NN) architectures for inference of AC-OPF solutions. Using fully connected NNs as a baseline we demonstrate the efficacy of leveraging network topology in models by constructing abstract representations of electrical grids in the graph domain for convolutional and graph NNs. The performance of the NN models is compared for both the direct (as regressors predicting optimal generator set-points) and indirect (as classifiers predicting the active set of constraints) approaches and computational gains for obtaining optimal solutions are also presented.