A Systematic Approach to Design Real-World Human-in-the-Loop Deep Reinforcement Learning: Salient Features, Challenges and Trade-offs

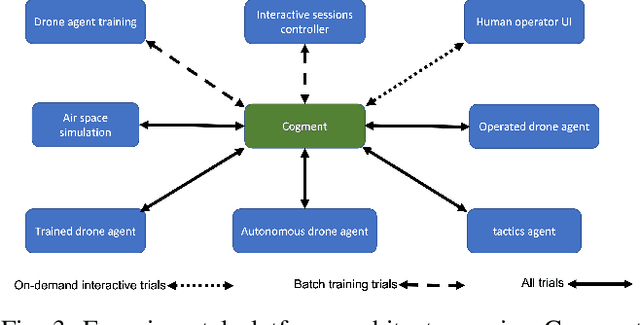
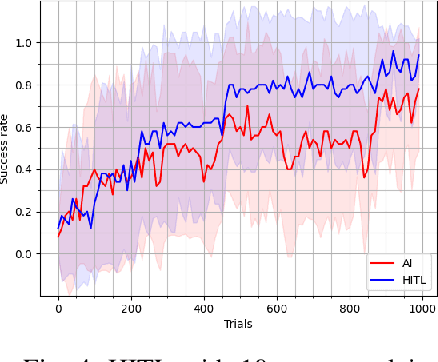
With the growing popularity of deep reinforcement learning (DRL), human-in-the-loop (HITL) approach has the potential to revolutionize the way we approach decision-making problems and create new opportunities for human-AI collaboration. In this article, we introduce a novel multi-layered hierarchical HITL DRL algorithm that comprises three types of learning: self learning, imitation learning and transfer learning. In addition, we consider three forms of human inputs: reward, action and demonstration. Furthermore, we discuss main challenges, trade-offs and advantages of HITL in solving complex problems and how human information can be integrated in the AI solution systematically. To verify our technical results, we present a real-world unmanned aerial vehicles (UAV) problem wherein a number of enemy drones attack a restricted area. The objective is to design a scalable HITL DRL algorithm for ally drones to neutralize the enemy drones before they reach the area. To this end, we first implement our solution using an award-winning open-source HITL software called Cogment. We then demonstrate several interesting results such as (a) HITL leads to faster training and higher performance, (b) advice acts as a guiding direction for gradient methods and lowers variance, and (c) the amount of advice should neither be too large nor too small to avoid over-training and under-training. Finally, we illustrate the role of human-AI cooperation in solving two real-world complex scenarios, i.e., overloaded and decoy attacks.

Human-AI Collaboration in Real-World Complex Environment with Reinforcement Learning

Recent advances in reinforcement learning (RL) and Human-in-the-Loop (HitL) learning have made human-AI collaboration easier for humans to team with AI agents. Leveraging human expertise and experience with AI in intelligent systems can be efficient and beneficial. Still, it is unclear to what extent human-AI collaboration will be successful, and how such teaming performs compared to humans or AI agents only. In this work, we show that learning from humans is effective and that human-AI collaboration outperforms human-controlled and fully autonomous AI agents in a complex simulation environment. In addition, we have developed a new simulator for critical infrastructure protection, focusing on a scenario where AI-powered drones and human teams collaborate to defend an airport against enemy drone attacks. We develop a user interface to allow humans to assist AI agents effectively. We demonstrated that agents learn faster while learning from policy correction compared to learning from humans or agents. Furthermore, human-AI collaboration requires lower mental and temporal demands, reduces human effort, and yields higher performance than if humans directly controlled all agents. In conclusion, we show that humans can provide helpful advice to the RL agents, allowing them to improve learning in a multi-agent setting.

Reinforcement Learning in Linear Quadratic Deep Structured Teams: Global Convergence of Policy Gradient Methods

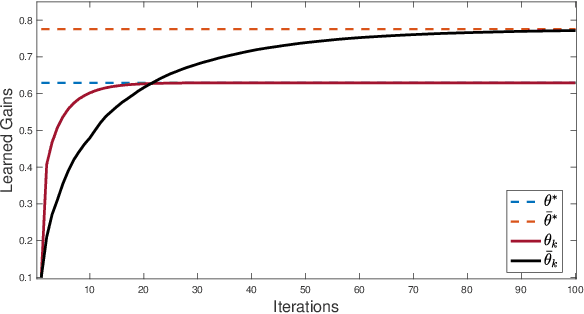
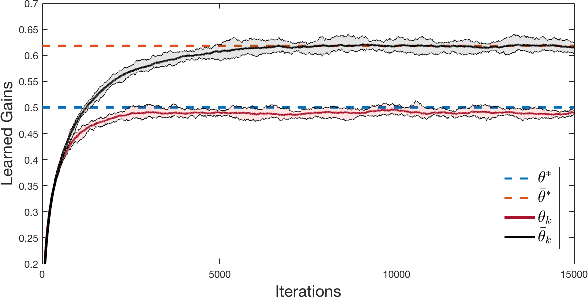
In this paper, we study the global convergence of model-based and model-free policy gradient descent and natural policy gradient descent algorithms for linear quadratic deep structured teams. In such systems, agents are partitioned into a few sub-populations wherein the agents in each sub-population are coupled in the dynamics and cost function through a set of linear regressions of the states and actions of all agents. Every agent observes its local state and the linear regressions of states, called deep states. For a sufficiently small risk factor and/or sufficiently large population, we prove that model-based policy gradient methods globally converge to the optimal solution. Given an arbitrary number of agents, we develop model-free policy gradient and natural policy gradient algorithms for the special case of risk-neutral cost function. The proposed algorithms are scalable with respect to the number of agents due to the fact that the dimension of their policy space is independent of the number of agents in each sub-population. Simulations are provided to verify the theoretical results.