Reinforcement Learning in Linear Quadratic Deep Structured Teams: Global Convergence of Policy Gradient Methods
Paper and Code
Dec 15, 2020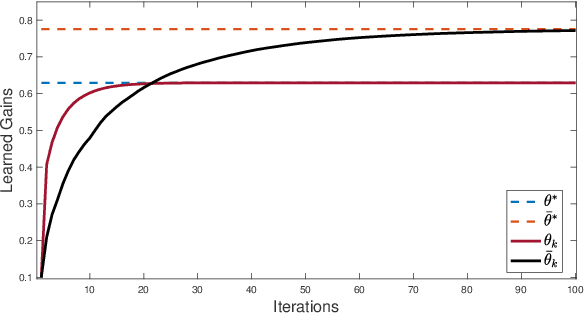
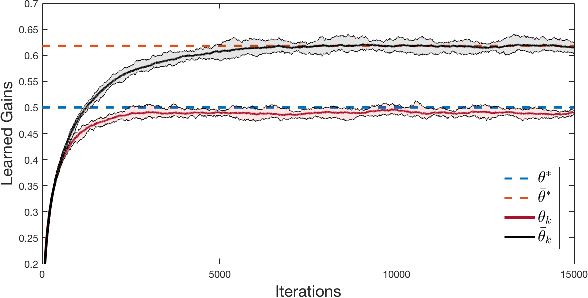
In this paper, we study the global convergence of model-based and model-free policy gradient descent and natural policy gradient descent algorithms for linear quadratic deep structured teams. In such systems, agents are partitioned into a few sub-populations wherein the agents in each sub-population are coupled in the dynamics and cost function through a set of linear regressions of the states and actions of all agents. Every agent observes its local state and the linear regressions of states, called deep states. For a sufficiently small risk factor and/or sufficiently large population, we prove that model-based policy gradient methods globally converge to the optimal solution. Given an arbitrary number of agents, we develop model-free policy gradient and natural policy gradient algorithms for the special case of risk-neutral cost function. The proposed algorithms are scalable with respect to the number of agents due to the fact that the dimension of their policy space is independent of the number of agents in each sub-population. Simulations are provided to verify the theoretical results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge