Prove Symbolic Regression is NP-hard by Symbol Graph

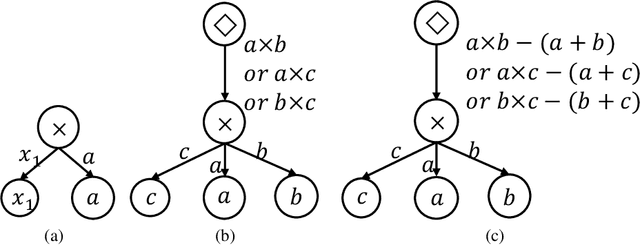
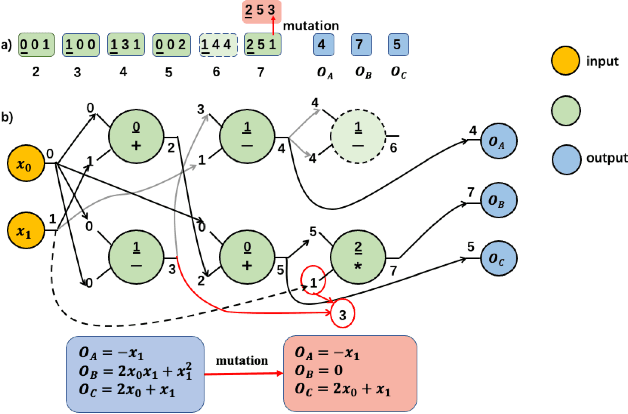
Symbolic regression (SR) is the task of discovering a symbolic expression that fits a given data set from the space of mathematical expressions. Despite the abundance of research surrounding the SR problem, there's a scarcity of works that confirm its NP-hard nature. Therefore, this paper introduces the concept of a symbol graph as a comprehensive representation of the entire mathematical expression space, effectively illustrating the NP-hard characteristics of the SR problem. Leveraging the symbol graph, we establish a connection between the SR problem and the task of identifying an optimally fitted degree-constrained Steiner Arborescence (DCSAP). The complexity of DCSAP, which is proven to be NP-hard, directly implies the NP-hard nature of the SR problem.

Exploring Hidden Semantics in Neural Networks with Symbolic Regression

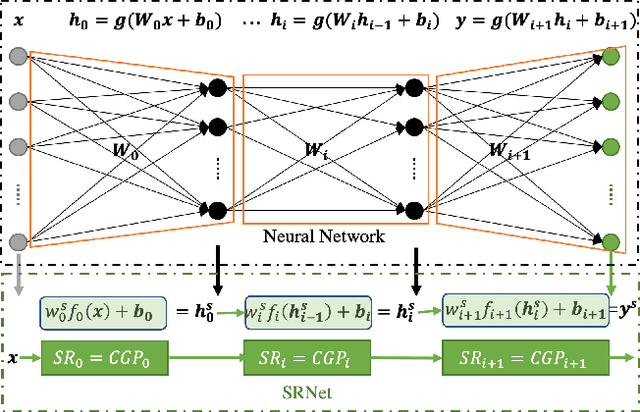
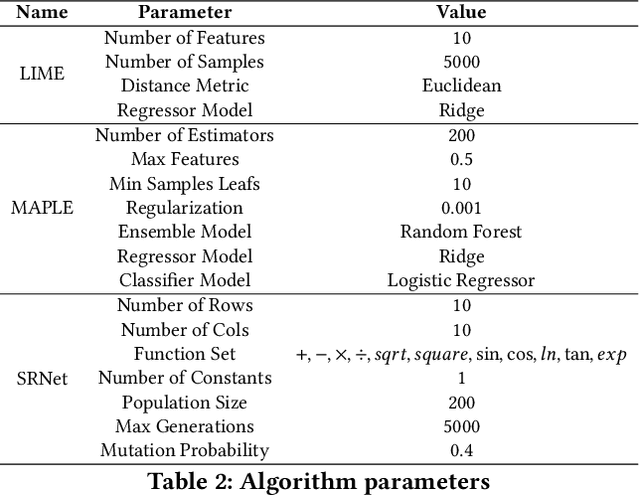
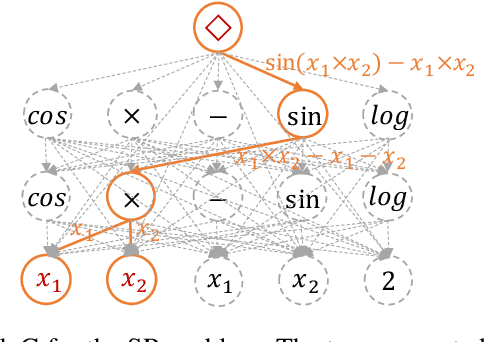
Many recent studies focus on developing mechanisms to explain the black-box behaviors of neural networks (NNs). However, little work has been done to extract the potential hidden semantics (mathematical representation) of a neural network. A succinct and explicit mathematical representation of a NN model could improve the understanding and interpretation of its behaviors. To address this need, we propose a novel symbolic regression method for neural works (called SRNet) to discover the mathematical expressions of a NN. SRNet creates a Cartesian genetic programming (NNCGP) to represent the hidden semantics of a single layer in a NN. It then leverages a multi-chromosome NNCGP to represent hidden semantics of all layers of the NN. The method uses a (1+$\lambda$) evolutionary strategy (called MNNCGP-ES) to extract the final mathematical expressions of all layers in the NN. Experiments on 12 symbolic regression benchmarks and 5 classification benchmarks show that SRNet not only can reveal the complex relationships between each layer of a NN but also can extract the mathematical representation of the whole NN. Compared with LIME and MAPLE, SRNet has higher interpolation accuracy and trends to approximate the real model on the practical dataset.

A Deep Learning Study on Osteosarcoma Detection from Histological Images

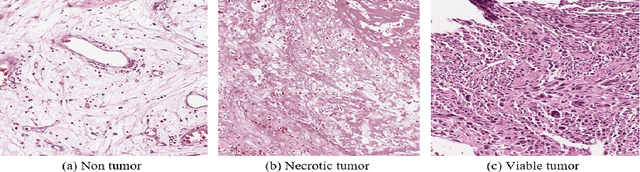
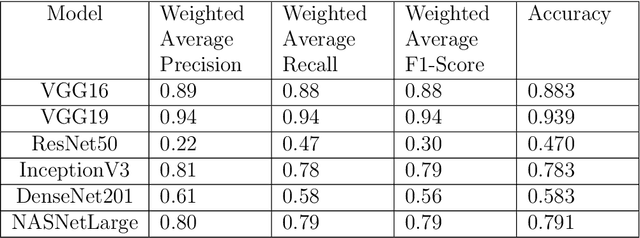
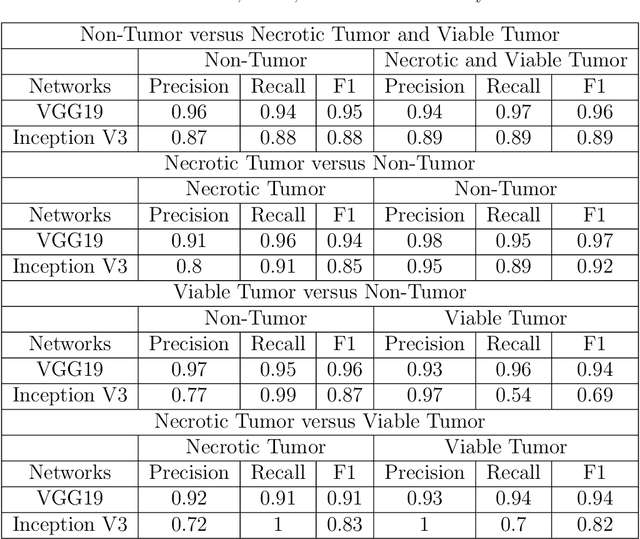
In the U.S, 5-10\% of new pediatric cases of cancer are primary bone tumors. The most common type of primary malignant bone tumor is osteosarcoma. The intention of the present work is to improve the detection and diagnosis of osteosarcoma using computer-aided detection (CAD) and diagnosis (CADx). Such tools as convolutional neural networks (CNNs) can significantly decrease the surgeon's workload and make a better prognosis of patient conditions. CNNs need to be trained on a large amount of data in order to achieve a more trustworthy performance. In this study, transfer learning techniques, pre-trained CNNs, are adapted to a public dataset on osteosarcoma histological images to detect necrotic images from non-necrotic and healthy tissues. First, the dataset was preprocessed, and different classifications are applied. Then, Transfer learning models including VGG19 and Inception V3 are used and trained on Whole Slide Images (WSI) with no patches, to improve the accuracy of the outputs. Finally, the models are applied to different classification problems, including binary and multi-class classifiers. Experimental results show that the accuracy of the VGG19 has the highest, 96\%, performance amongst all binary classes and multiclass classification. Our fine-tuned model demonstrates state-of-the-art performance on detecting malignancy of Osteosarcoma based on histologic images.