Prove Symbolic Regression is NP-hard by Symbol Graph
Paper and Code
Apr 22, 2024

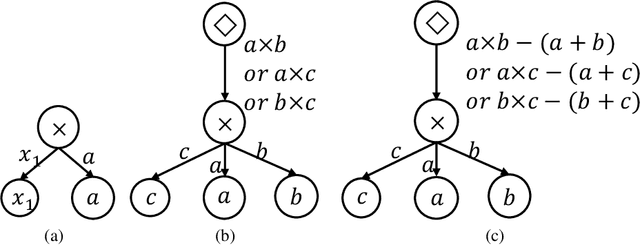
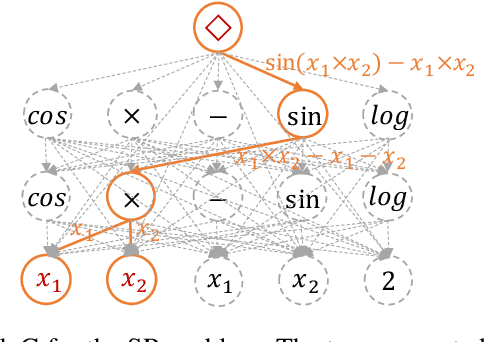
Symbolic regression (SR) is the task of discovering a symbolic expression that fits a given data set from the space of mathematical expressions. Despite the abundance of research surrounding the SR problem, there's a scarcity of works that confirm its NP-hard nature. Therefore, this paper introduces the concept of a symbol graph as a comprehensive representation of the entire mathematical expression space, effectively illustrating the NP-hard characteristics of the SR problem. Leveraging the symbol graph, we establish a connection between the SR problem and the task of identifying an optimally fitted degree-constrained Steiner Arborescence (DCSAP). The complexity of DCSAP, which is proven to be NP-hard, directly implies the NP-hard nature of the SR problem.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge