Unified Long-Term Time-Series Forecasting Benchmark

In order to support the advancement of machine learning methods for predicting time-series data, we present a comprehensive dataset designed explicitly for long-term time-series forecasting. We incorporate a collection of datasets obtained from diverse, dynamic systems and real-life records. Each dataset is standardized by dividing it into training and test trajectories with predetermined lookback lengths. We include trajectories of length up to $2000$ to ensure a reliable evaluation of long-term forecasting capabilities. To determine the most effective model in diverse scenarios, we conduct an extensive benchmarking analysis using classical and state-of-the-art models, namely LSTM, DeepAR, NLinear, N-Hits, PatchTST, and LatentODE. Our findings reveal intriguing performance comparisons among these models, highlighting the dataset-dependent nature of model effectiveness. Notably, we introduce a custom latent NLinear model and enhance DeepAR with a curriculum learning phase. Both consistently outperform their vanilla counterparts.

Worrisome Properties of Neural Network Controllers and Their Symbolic Representations

We raise concerns about controllers' robustness in simple reinforcement learning benchmark problems. We focus on neural network controllers and their low neuron and symbolic abstractions. A typical controller reaching high mean return values still generates an abundance of persistent low-return solutions, which is a highly undesirable property, easily exploitable by an adversary. We find that the simpler controllers admit more persistent bad solutions. We provide an algorithm for a systematic robustness study and prove existence of persistent solutions and, in some cases, periodic orbits, using a computer-assisted proof methodology.

Improved Overparametrization Bounds for Global Convergence of Stochastic Gradient Descent for Shallow Neural Networks

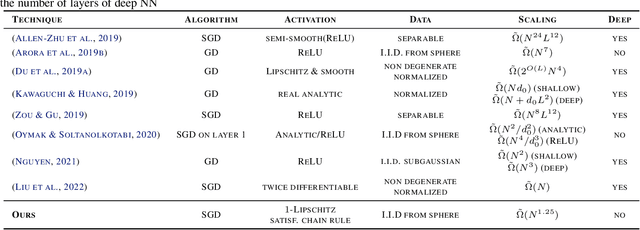
We study the overparametrization bounds required for the global convergence of stochastic gradient descent algorithm for a class of one hidden layer feed-forward neural networks, considering most of the activation functions used in practice, including ReLU. We improve the existing state-of-the-art results in terms of the required hidden layer width. We introduce a new proof technique combining nonlinear analysis with properties of random initializations of the network. First, we establish the global convergence of continuous solutions of the differential inclusion being a nonsmooth analogue of the gradient flow for the MSE loss. Second, we provide a technical result (working also for general approximators) relating solutions of the aforementioned differential inclusion to the (discrete) stochastic gradient descent sequences, hence establishing linear convergence towards zero loss for the stochastic gradient descent iterations.

On The Verification of Neural ODEs with Stochastic Guarantees

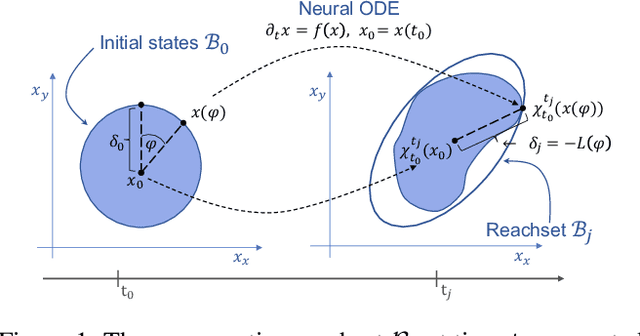
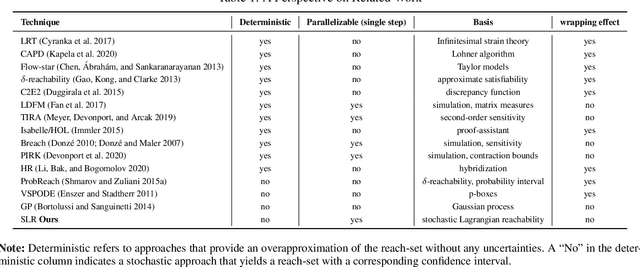
We show that Neural ODEs, an emerging class of time-continuous neural networks, can be verified by solving a set of global-optimization problems. For this purpose, we introduce Stochastic Lagrangian Reachability (SLR), an abstraction-based technique for constructing a tight Reachtube (an over-approximation of the set of reachable states over a given time-horizon), and provide stochastic guarantees in the form of confidence intervals for the Reachtube bounds. SLR inherently avoids the infamous wrapping effect (accumulation of over-approximation errors) by performing local optimization steps to expand safe regions instead of repeatedly forward-propagating them as is done by deterministic reachability methods. To enable fast local optimizations, we introduce a novel forward-mode adjoint sensitivity method to compute gradients without the need for backpropagation. Finally, we establish asymptotic and non-asymptotic convergence rates for SLR.

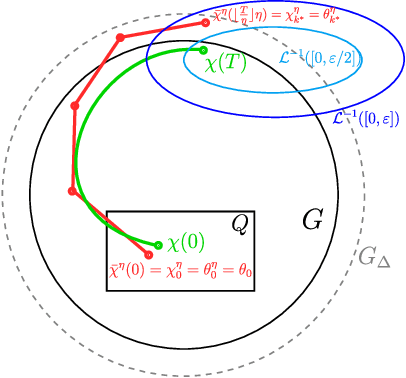
Lagrangian Reachtubes: The Next Generation

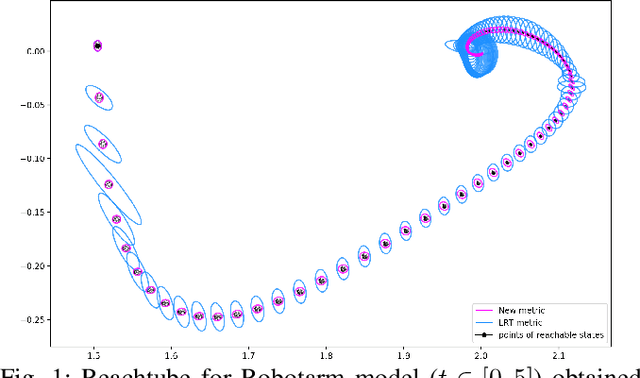
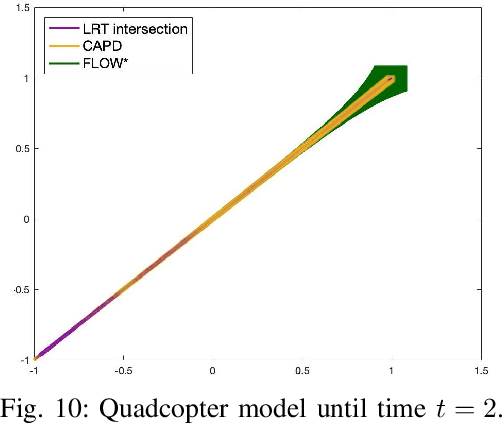
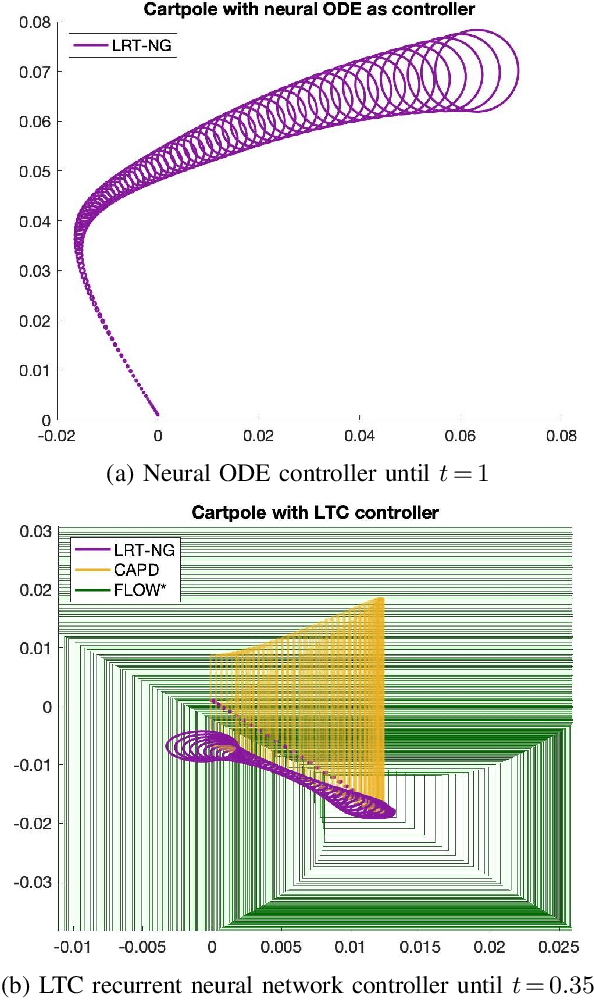
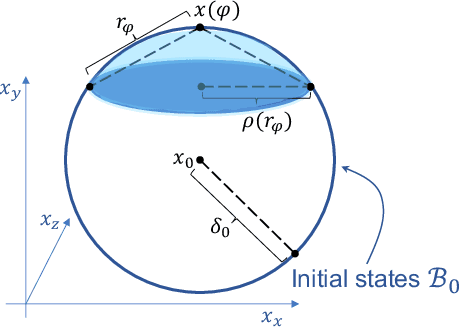
We introduce LRT-NG, a set of techniques and an associated toolset that computes a reachtube (an over-approximation of the set of reachable states over a given time horizon) of a nonlinear dynamical system. LRT-NG significantly advances the state-of-the-art Langrangian Reachability and its associated tool LRT. From a theoretical perspective, LRT-NG is superior to LRT in three ways. First, it uses for the first time an analytically computed metric for the propagated ball which is proven to minimize the ball's volume. We emphasize that the metric computation is the centerpiece of all bloating-based techniques. Secondly, it computes the next reachset as the intersection of two balls: one based on the Cartesian metric and the other on the new metric. While the two metrics were previously considered opposing approaches, their joint use considerably tightens the reachtubes. Thirdly, it avoids the "wrapping effect" associated with the validated integration of the center of the reachset, by optimally absorbing the interval approximation in the radius of the next ball. From a tool-development perspective, LRT-NG is superior to LRT in two ways. First, it is a standalone tool that no longer relies on CAPD. This required the implementation of the Lohner method and a Runge-Kutta time-propagation method. Secondly, it has an improved interface, allowing the input model and initial conditions to be provided as external input files. Our experiments on a comprehensive set of benchmarks, including two Neural ODEs, demonstrates LRT-NG's superior performance compared to LRT, CAPD, and Flow*.

Mapper Based Classifier

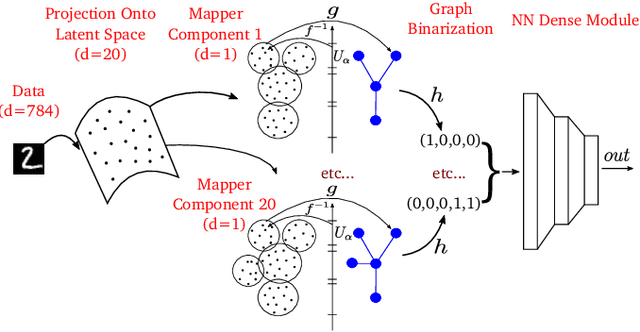
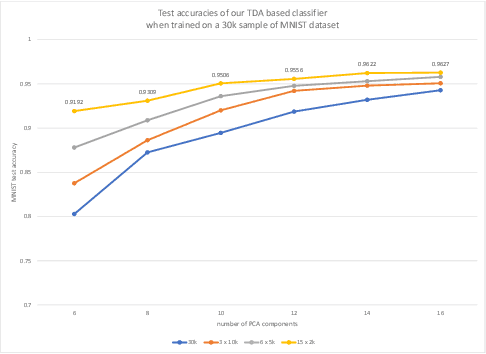
Topological data analysis aims to extract topological quantities from data, which tend to focus on the broader global structure of the data rather than local information. The Mapper method, specifically, generalizes clustering methods to identify significant global mathematical structures, which are out of reach of many other approaches. We propose a classifier based on applying the Mapper algorithm to data projected onto a latent space. We obtain the latent space by using PCA or autoencoders. Notably, a classifier based on the Mapper method is immune to any gradient based attack, and improves robustness over traditional CNNs (convolutional neural networks). We report theoretical justification and some numerical experiments that confirm our claims.