Sequential Topological Representations for Predictive Models of Deformable Objects

Deformable objects present a formidable challenge for robotic manipulation due to the lack of canonical low-dimensional representations and the difficulty of capturing, predicting, and controlling such objects. We construct compact topological representations to capture the state of highly deformable objects that are topologically nontrivial. We develop an approach that tracks the evolution of this topological state through time. Under several mild assumptions, we prove that the topology of the scene and its evolution can be recovered from point clouds representing the scene. Our further contribution is a method to learn predictive models that take a sequence of past point cloud observations as input and predict a sequence of topological states, conditioned on target/future control actions. Our experiments with highly deformable objects in simulation show that the proposed multistep predictive models yield more precise results than those obtained from computational topology libraries. These models can leverage patterns inferred across various objects and offer fast multistep predictions suitable for real-time applications.

The effect of Target Normalization and Momentum on Dying ReLU

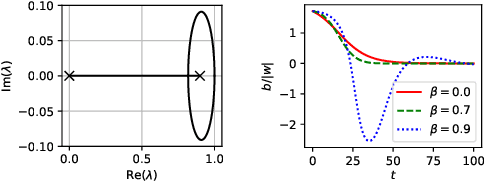
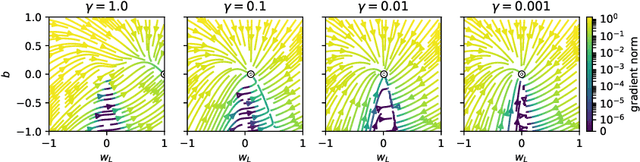
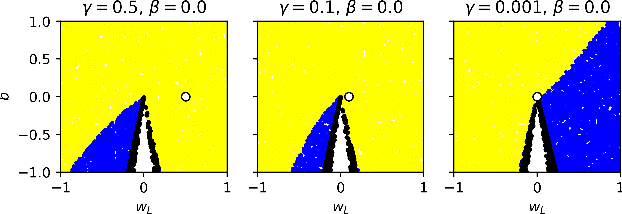
Optimizing parameters with momentum, normalizing data values, and using rectified linear units (ReLUs) are popular choices in neural network (NN) regression. Although ReLUs are popular, they can collapse to a constant function and "die", effectively removing their contribution from the model. While some mitigations are known, the underlying reasons of ReLUs dying during optimization are currently poorly understood. In this paper, we consider the effects of target normalization and momentum on dying ReLUs. We find empirically that unit variance targets are well motivated and that ReLUs die more easily, when target variance approaches zero. To further investigate this matter, we analyze a discrete-time linear autonomous system, and show theoretically how this relates to a model with a single ReLU and how common properties can result in dying ReLU. We also analyze the gradients of a single-ReLU model to identify saddle points and regions corresponding to dying ReLU and how parameters evolve into these regions when momentum is used. Finally, we show empirically that this problem persist, and is aggravated, for deeper models including residual networks.

Free Space of Rigid Objects: Caging, Path Non-Existence, and Narrow Passage Detection

In this work we propose algorithms to explicitly construct a conservative estimate of the configuration spaces of rigid objects in 2D and 3D. Our approach is able to detect compact path components and narrow passages in configuration space which are important for applications in robotic manipulation and path planning. Moreover, as we demonstrate, they are also applicable to identification of molecular cages in chemistry. Our algorithms are based on a decomposition of the resulting 3 and 6 dimensional configuration spaces into slices corresponding to a finite sample of fixed orientations in configuration space. We utilize dual diagrams of unions of balls and uniform grids of orientations to approximate the configuration space. We carry out experiments to evaluate the computational efficiency on a set of objects with different geometric features thus demonstrating that our approach is applicable to different object shapes. We investigate the performance of our algorithm by computing increasingly fine-grained approximations of the object's configuration space.

A Decomposition-Based Approach to Reasoning about Free Space Path-Connectivity for Rigid Objects in 2D

In this paper, we compute a conservative approximation of the path-connected components of the free space of a rigid object in a 2D workspace in order to solve two closely related problems: to determine whether there exists a collision-free path between two given configurations, and to verify whether an object can escape arbitrarily far from its initial configuration -- i.e., whether the object is caged. Furthermore, we consider two quantitative characteristics of the free space: the volume of path-connected components and the width of narrow passages. To address these problems, we decompose the configuration space into a set of two-dimensional slices, approximate them as two-dimensional alpha-complexes, and then study the relations between them. This significantly reduces the computational complexity compared to a direct approximation of the free space. We implement our algorithm and run experiments in a three-dimensional configuration space of a simple object showing runtime of less than 2 seconds.