Predicting Instability in Complex Oscillator Networks: Limitations and Potentials of Network Measures and Machine Learning

A central question of network science is how functional properties of systems arise from their structure. For networked dynamical systems, structure is typically quantified with network measures. A functional property that is of theoretical and practical interest for oscillatory systems is the stability of synchrony to localized perturbations. Recently, Graph Neural Networks (GNNs) have been shown to predict this stability successfully; at the same time, network measures have struggled to paint a clear picture. Here we collect 46 relevant network measures and find that no small subset can reliably predict stability. The performance of GNNs can only be matched by combining all network measures and nodewise machine learning. However, unlike GNNs, this approach fails to extrapolate from network ensembles to several real power grid topologies. This suggests that correlations of network measures and function may be misleading, and that GNNs capture the causal relationship between structure and stability substantially better.

Federated Learning in Wireless Networks via Over-the-Air Computations

In a multi-agent system, agents can cooperatively learn a model from data by exchanging their estimated model parameters, without the need to exchange the locally available data used by the agents. This strategy, often called federated learning, is mainly employed for two reasons: (i) improving resource-efficiency by avoiding to share potentially large datasets and (ii) guaranteeing privacy of local agents' data. Efficiency can be further increased by adopting a beyond-5G communication strategy that goes under the name of Over-the-Air Computation. This strategy exploits the interference property of the wireless channel. Standard communication schemes prevent interference by enabling transmissions of signals from different agents at distinct time or frequency slots, which is not required with Over-the-Air Computation, thus saving resources. In this case, the received signal is a weighted sum of transmitted signals, with unknown weights (fading channel coefficients). State of the art papers in the field aim at reconstructing those unknown coefficients. In contrast, the approach presented here does not require reconstructing channel coefficients by complex encoding-decoding schemes. This improves both efficiency and privacy.

Optimal control for a robotic exploration, pick-up and delivery problem

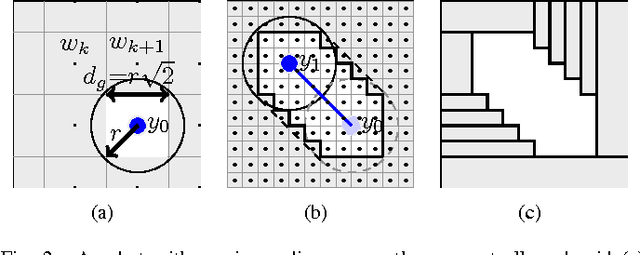
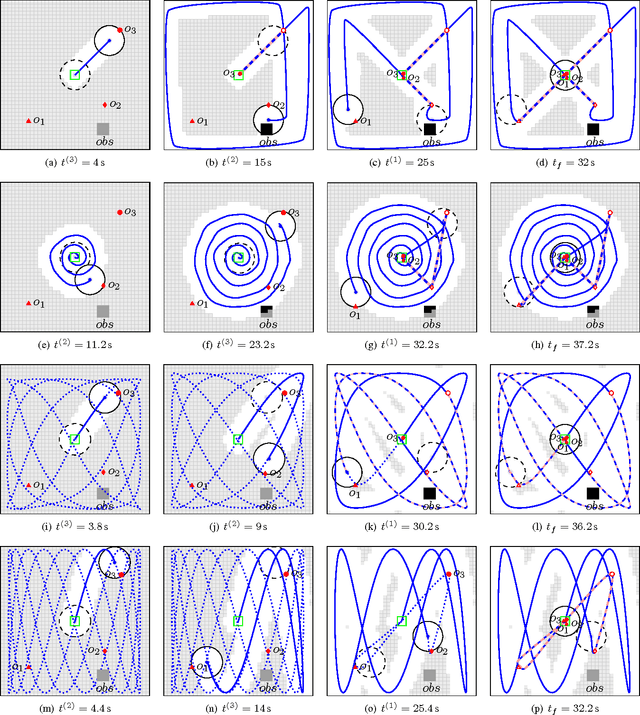
This paper addresses an optimal control problem for a robot that has to find and collect a finite number of objects and move them to a depot in minimum time. The robot has fourth-order dynamics that change instantaneously at any pick-up or drop-off of an object. The objects are modeled by point masses with a-priori unknown locations in a bounded two-dimensional space that may contain unknown obstacles. For this hybrid system, an Optimal Control Problem (OCP) is approximately solved by a receding horizon scheme, where the derived lower bound for the cost-to-go is evaluated for the worst and for a probabilistic case, assuming a uniform distribution of the objects. First, a time-driven approximate solution based on time and position space discretization and mixed integer programming is presented. Due to the high computational cost of this solution, an alternative event-driven approximate approach based on a suitable motion parameterization and gradient-based optimization is proposed. The solutions are compared in a numerical example, suggesting that the latter approach offers a significant computational advantage while yielding similar qualitative results compared to the former. The methods are particularly relevant for various robotic applications like automated cleaning, search and rescue, harvesting or manufacturing.