Optimal control for a robotic exploration, pick-up and delivery problem
Paper and Code
Jul 05, 2016
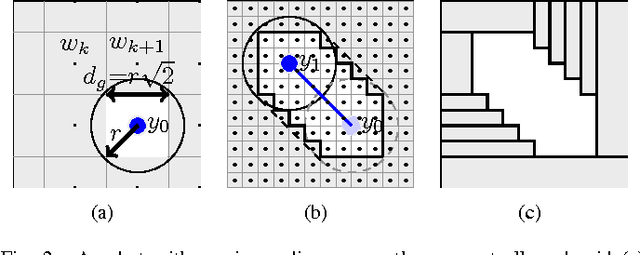

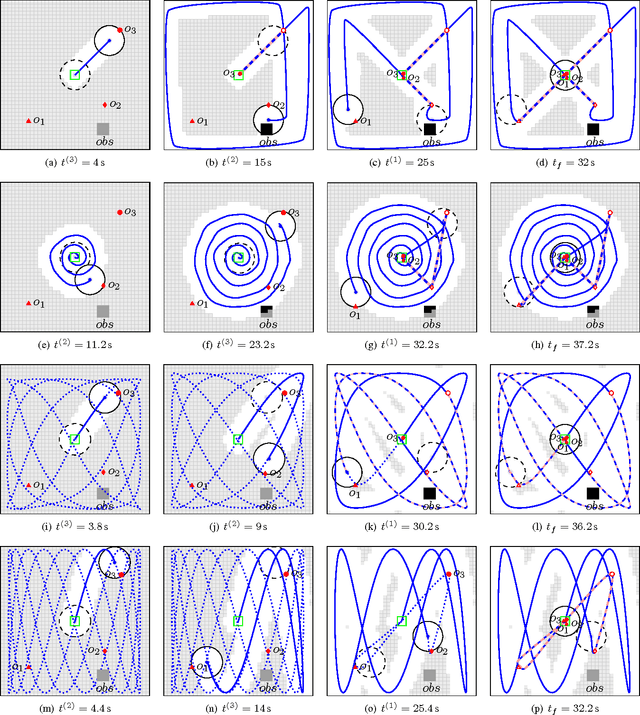
This paper addresses an optimal control problem for a robot that has to find and collect a finite number of objects and move them to a depot in minimum time. The robot has fourth-order dynamics that change instantaneously at any pick-up or drop-off of an object. The objects are modeled by point masses with a-priori unknown locations in a bounded two-dimensional space that may contain unknown obstacles. For this hybrid system, an Optimal Control Problem (OCP) is approximately solved by a receding horizon scheme, where the derived lower bound for the cost-to-go is evaluated for the worst and for a probabilistic case, assuming a uniform distribution of the objects. First, a time-driven approximate solution based on time and position space discretization and mixed integer programming is presented. Due to the high computational cost of this solution, an alternative event-driven approximate approach based on a suitable motion parameterization and gradient-based optimization is proposed. The solutions are compared in a numerical example, suggesting that the latter approach offers a significant computational advantage while yielding similar qualitative results compared to the former. The methods are particularly relevant for various robotic applications like automated cleaning, search and rescue, harvesting or manufacturing.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge