Label-independent hyperparameter-free self-supervised single-view deep subspace clustering

Deep subspace clustering (DSC) algorithms face several challenges that hinder their widespread adoption across variois application domains. First, clustering quality is typically assessed using only the encoder's output layer, disregarding valuable information present in the intermediate layers. Second, most DSC approaches treat representation learning and subspace clustering as independent tasks, limiting their effectiveness. Third, they assume the availability of a held-out dataset for hyperparameter tuning, which is often impractical in real-world scenarios. Fourth, learning termination is commonly based on clustering error monitoring, requiring external labels. Finally, their performance often depends on post-processing techniques that rely on labeled data. To address this limitations, we introduce a novel single-view DSC approach that: (i) minimizes a layer-wise self expression loss using a joint representation matrix; (ii) optimizes a subspace-structured norm to enhance clustering quality; (iii) employs a multi-stage sequential learning framework, consisting of pre-training and fine-tuning, enabling the use of multiple regularization terms without hyperparameter tuning; (iv) incorporates a relative error-based self-stopping mechanism to terminate training without labels; and (v) retains a fixed number of leading coefficients in the learned representation matrix based on prior knowledge. We evaluate the proposed method on six datasets representing faces, digits, and objects. The results show that our method outperforms most linear SC algorithms with careffulyl tuned hyperparameters while maintaining competitive performance with the best performing linear appoaches.

Interpretable label-free self-guided subspace clustering

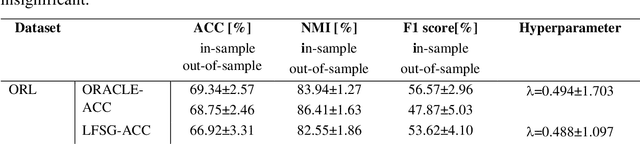
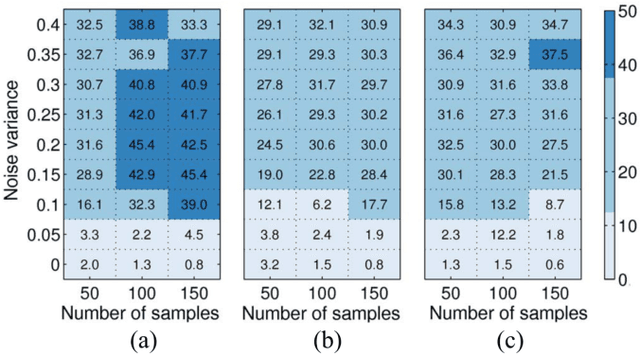
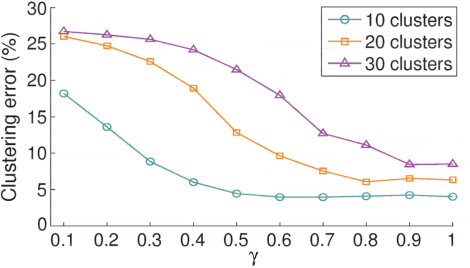
Majority subspace clustering (SC) algorithms depend on one or more hyperparameters that need to be carefully tuned for the SC algorithms to achieve high clustering performance. Hyperparameter optimization (HPO) is often performed using grid-search, assuming that some labeled data is available. In some domains, such as medicine, this assumption does not hold true in many cases. One avenue of research focuses on developing SC algorithms that are inherently free of hyperparameters. For hyperparameters-dependent SC algorithms, one approach to label-independent HPO tuning is based on internal clustering quality metrics (if available), whose performance should ideally match that of external (label-dependent) clustering quality metrics. In this paper, we propose a novel approach to label-independent HPO that uses clustering quality metrics, such as accuracy (ACC) or normalized mutual information (NMI), that are computed based on pseudo-labels obtained from the SC algorithm across a predefined grid of hyperparameters. Assuming that ACC (or NMI) is a smooth function of hyperparameter values it is possible to select subintervals of hyperparameters. These subintervals are then iteratively further split into halves or thirds until a relative error criterion is satisfied. In principle, the hyperparameters of any SC algorithm can be tuned using the proposed method. We demonstrate this approach on several single- and multi-view SC algorithms, comparing the achieved performance with their oracle versions across six datasets representing digits, faces and objects. The proposed method typically achieves clustering performance that is 5% to 7% lower than that of the oracle versions. We also make our proposed method interpretable by visualizing subspace bases, which are estimated from the computed clustering partitions. This aids in the initial selection of the hyperparameter search space.

A Hyperspectral Imaging Dataset and Methodology for Intraoperative Pixel-Wise Classification of Metastatic Colon Cancer in the Liver

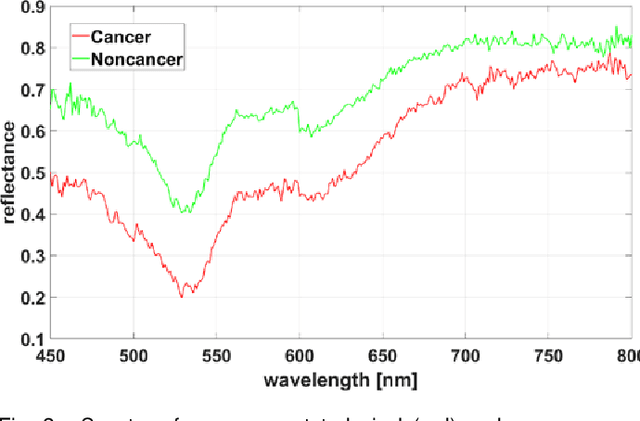
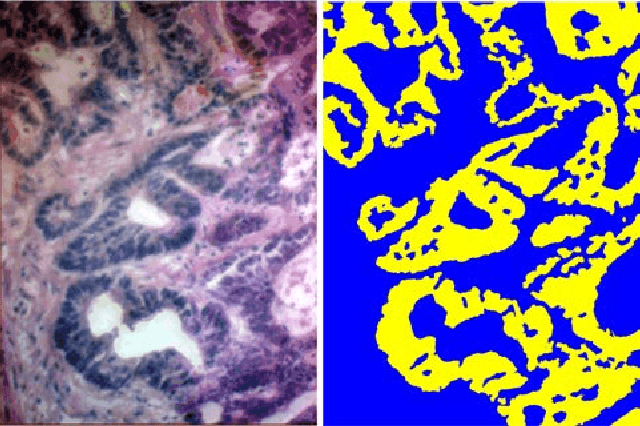
Hyperspectral imaging (HSI) holds significant potential for transforming the field of computational pathology. However, there is currently a shortage of pixel-wise annotated HSI data necessary for training deep learning (DL) models. Additionally, the number of HSI-based research studies remains limited, and in many cases, the advantages of HSI over traditional RGB imaging have not been conclusively demonstrated, particularly for specimens collected intraoperatively. To address these challenges we present a database consisted of 27 HSIs of hematoxylin-eosin stained frozen sections, collected from 14 patients with colon adenocarcinoma metastasized to the liver. It is aimed to validate pixel-wise classification for intraoperative tumor resection. The HSIs were acquired in the spectral range of 450 to 800 nm, with a resolution of 1 nm, resulting in images of 1384x1035 pixels. Pixel-wise annotations were performed by three pathologists. To overcome challenges such as experimental variability and the lack of annotated data, we combined label-propagation-based semi-supervised learning (SSL) with spectral-spatial features extracted by: the multiscale principle of relevant information (MPRI) method and tensor singular spectrum analysis method. Using only 1% of labeled pixels per class the SSL-MPRI method achieved a micro balanced accuracy (BACC) of 0.9313 and a micro F1-score of 0.9235 on the HSI dataset. The performance on corresponding RGB images was lower, with a micro BACC of 0.8809 and a micro F1-score of 0.8688. These improvements are statistically significant. The SSL-MPRI approach outperformed six DL architectures trained with 63% of labeled pixels. Data and code are available at: https://github.com/ikopriva/ColonCancerHSI.

Subspace Clustering in Wavelet Packets Domain

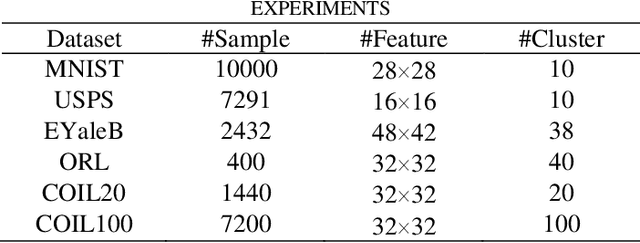
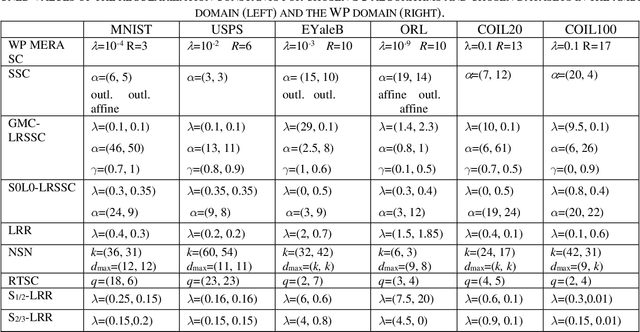
Subspace clustering (SC) algorithms utilize the union of subspaces model to cluster data points according to the subspaces from which they are drawn. To better address separability of subspaces and robustness to noise we propose a wavelet packet (WP) based transform domain subspace clustering. Depending on the number of resolution levels, WP yields several representations instantiated in terms of subbands. The first approach combines original and subband data into one complementary multi-view representation. Afterward, we formulate joint representation learning as a low-rank MERA tensor network approximation problem. That is motivated by the strong representation power of the MERA network to capture complex intra/inter-view dependencies in corresponding self-representation tensor. In the second approach, we use a self-stopping computationally efficient method to select the subband with the smallest clustering error on the validation set. When existing SC algorithms are applied to the chosen subband, their performance is expected to improve. Consequently, both approaches enable the re-use of SC algorithms developed so far. Improved clustering performance is due to the dual nature of subbands as representations and filters, which is essential for noise suppression. We exemplify the proposed WP domain approach to SC on the MERA tensor network and eight other well-known linear SC algorithms using six well-known image datasets representing faces, digits, and objects. Although WP domain-based SC is a linear method, it achieved clustering performance comparable with some best deep SC algorithms and outperformed many other deep SC algorithms by a significant margin. That is in particular case for the WP MERA SC algorithm. On the COIL100 dataset, it achieves an accuracy of 87.45% and outperforms the best deep SC competitor in the amount of 14.75%.

Robust Kernel Sparse Subspace Clustering

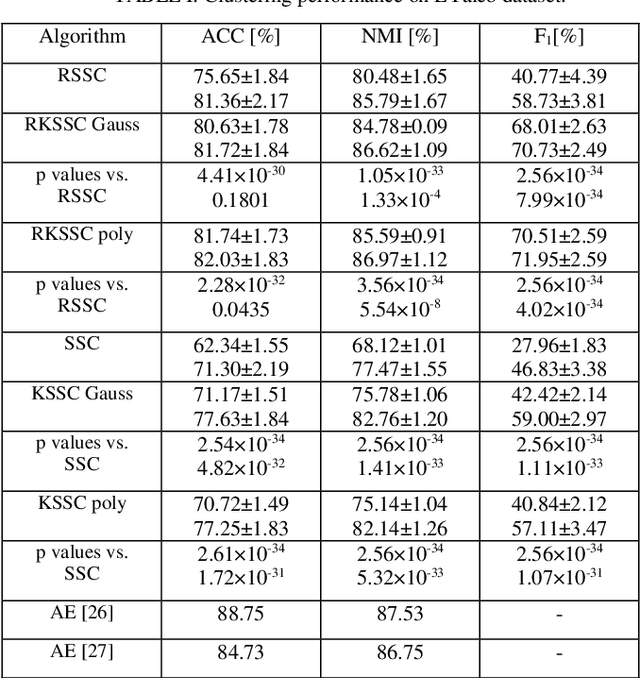
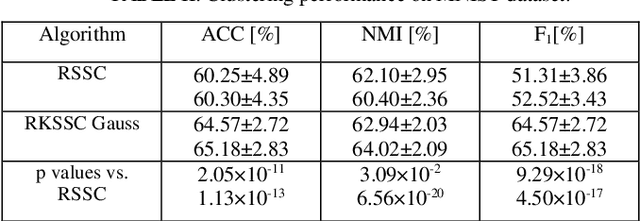
Kernel methods are applied to many problems in pattern recognition, including subspace clustering (SC). That way, nonlinear problems in the input data space become linear in mapped high-dimensional feature space. Thereby, computationally tractable nonlinear algorithms are enabled through implicit mapping by the virtue of kernel trick. However, kernelization of linear algorithms is possible only if square of the Froebenious norm of the error term is used in related optimization problem. That, however, implies normal distribution of the error. That is not appropriate for non-Gaussian errors such as gross sparse corruptions that are modeled by -norm. Herein, to the best of our knowledge, we propose for the first time robust kernel sparse SC (RKSSC) algorithm for data with gross sparse corruptions. The concept, in principle, can be applied to other SC algorithms to achieve robustness to the presence of such type of corruption. We validated proposed approach on two well-known datasets with linear robust SSC algorithm as a baseline model. According to Wilcoxon test, clustering performance obtained by the RKSSC algorithm is statistically significantly better than corresponding performance obtained by the robust SSC algorithm. MATLAB code of proposed RKSSC algorithm is posted on https://github.com/ikopriva/RKSSC.

Multilayer Graph Approach to Deep Subspace Clustering

Deep subspace clustering (DSC) networks based on self-expressive model learn representation matrix, often implemented in terms of fully connected network, in the embedded space. After the learning is finished, representation matrix is used by spectral clustering module to assign labels to clusters. However, such approach ignores complementary information that exist in other layers of the encoder (including the input data themselves). Herein, we apply selected linear subspace clustering algorithm to learn representation matrices from representations learned by all layers of encoder network including the input data. Afterward, we learn a multilayer graph that in a multi-view like manner integrates information from graph Laplacians of all used layers. That improves further performance of selected DSC network. Furthermore, we also provide formulation of our approach to cluster out-of-sample/test data points. We validate proposed approach on four well-known datasets with two DSC networks as baseline models. In almost all the cases, proposed approach achieved statistically significant improvement in three performance metrics. MATLAB code of proposed algorithm is posted on https://github.com/lovro-sinda/MLG-DSC.

LEFM-Nets: Learnable Explicit Feature Map Deep Networks for Segmentation of Histopathological Images of Frozen Sections

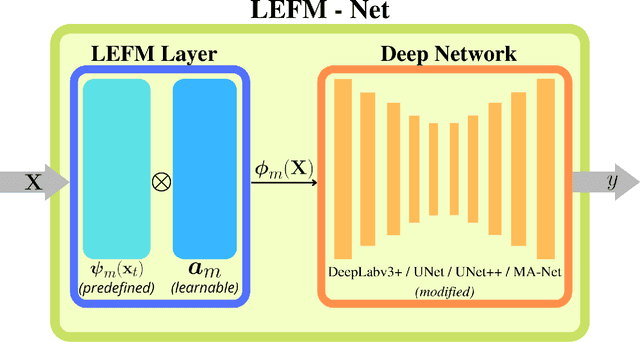
Accurate segmentation of medical images is essential for diagnosis and treatment of diseases. These problems are solved by highly complex models, such as deep networks (DN), requiring a large amount of labeled data for training. Thereby, many DNs possess task- or imaging modality specific architectures with a decision-making process that is often hard to explain and interpret. Here, we propose a framework that embeds existing DNs into a low-dimensional subspace induced by the learnable explicit feature map (LEFM) layer. Compared to the existing DN, the framework adds one hyperparameter and only modestly increase the number of learnable parameters. The method is aimed at, but not limited to, segmentation of low-dimensional medical images, such as color histopathological images of stained frozen sections. Since features in the LEFM layer are polynomial functions of the original features, proposed LEFM-Nets contribute to the interpretability of network decisions. In this work, we combined LEFM with the known networks: DeepLabv3+, UNet, UNet++ and MA-net. New LEFM-Nets are applied to the segmentation of adenocarcinoma of a colon in a liver from images of hematoxylin and eosin (H&E) stained frozen sections. LEFM-Nets are also tested on nuclei segmentation from images of H&E stained frozen sections of ten human organs. On the first problem, LEFM-Nets achieved statistically significant performance improvement in terms of micro balanced accuracy and $F_1$ score than original networks. LEFM-Nets achieved only better performance in comparison with the original networks on the second problem. The source code is available at https://github.com/dsitnik/lefm.

Clustering and classification of low-dimensional data in explicit feature map domain: intraoperative pixel-wise diagnosis of adenocarcinoma of a colon in a liver

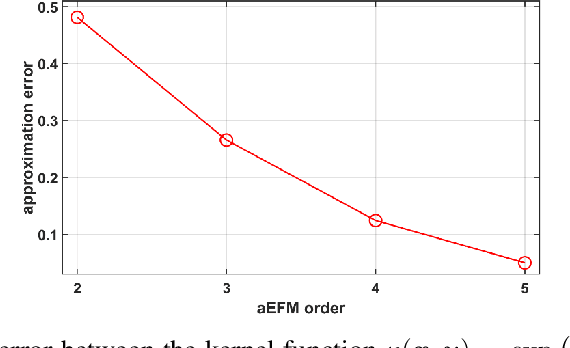
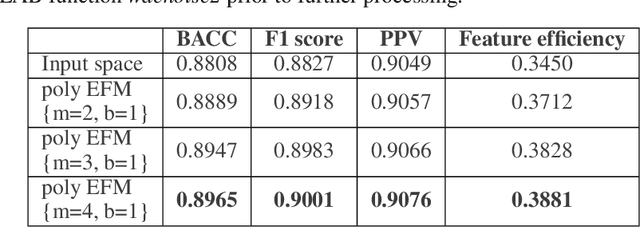
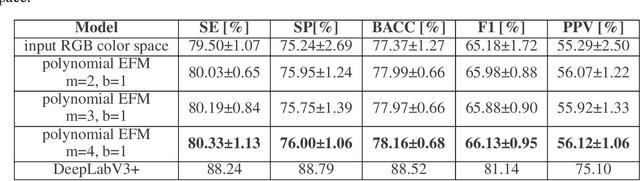
Application of artificial intelligence in medicine brings in highly accurate predictions achieved by complex models, the reasoning of which is hard to interpret. Their generalization ability can be reduced because of the lack of pixel wise annotated images that occurs in frozen section tissue analysis. To partially overcome this gap, this paper explores the approximate explicit feature map (aEFM) transform of low-dimensional data into a low-dimensional subspace in Hilbert space. There, with a modest increase in computational complexity, linear algorithms yield improved performance and keep interpretability. They remain amenable to incremental learning that is not a trivial issue for some nonlinear algorithms. We demonstrate proposed methodology on a very large-scale problem related to intraoperative pixel-wise semantic segmentation and clustering of adenocarcinoma of a colon in a liver. Compared to the results in the input space, logistic classifier achieved statistically significant performance improvements in micro balanced accuracy and F1 score in the amounts of 12.04% and 12.58%, respectively. Support vector machine classifier yielded the increase of 8.04% and 9.41%. For clustering, increases of 0.79% and 0.85% are obtained with ultra large-scale spectral clustering algorithm. Results are supported by a discussion of interpretability using Shapely additive explanation values for predictions of linear classifier in input space and aEFM induced space.

Robust Self-Supervised Convolutional Neural Network for Subspace Clustering and Classification

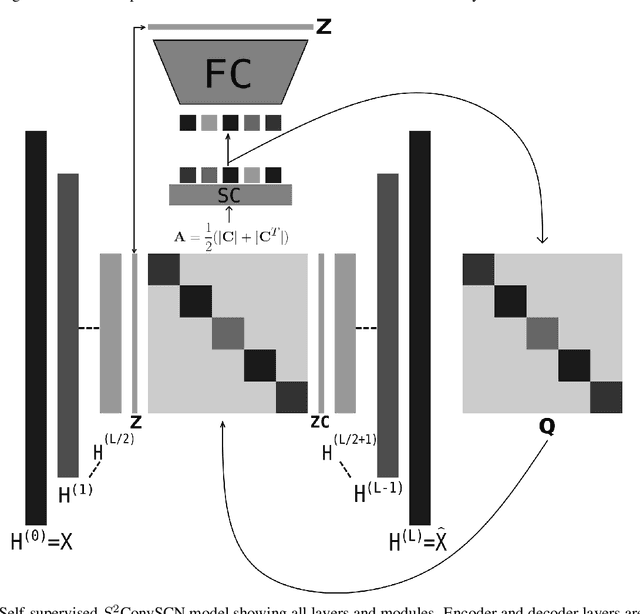
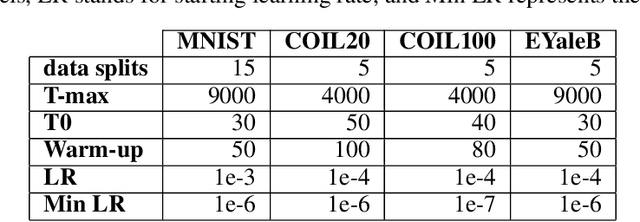
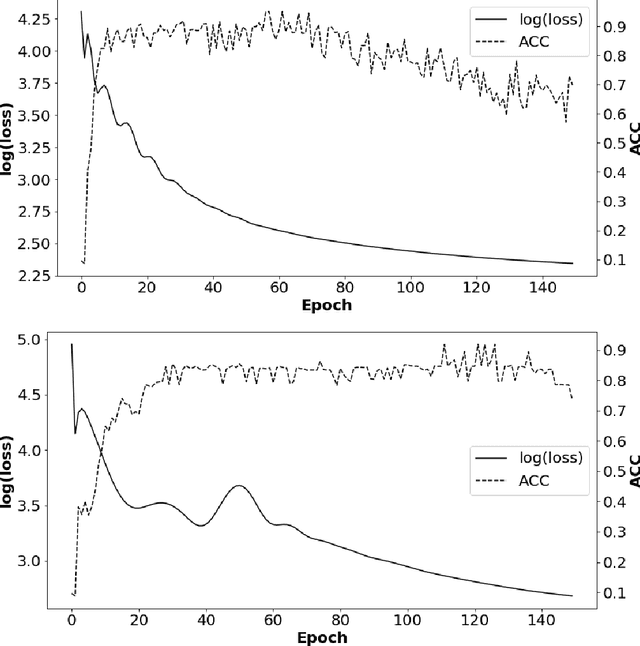
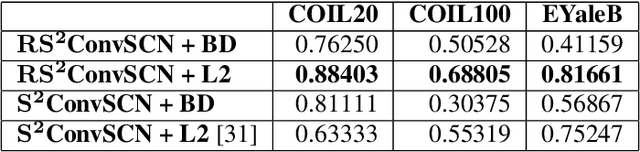
Insufficient capability of existing subspace clustering methods to handle data coming from nonlinear manifolds, data corruptions, and out-of-sample data hinders their applicability to address real-world clustering and classification problems. This paper proposes the robust formulation of the self-supervised convolutional subspace clustering network ($S^2$ConvSCN) that incorporates the fully connected (FC) layer and, thus, it is capable for handling out-of-sample data by classifying them using a softmax classifier. $S^2$ConvSCN clusters data coming from nonlinear manifolds by learning the linear self-representation model in the feature space. Robustness to data corruptions is achieved by using the correntropy induced metric (CIM) of the error. Furthermore, the block-diagonal (BD) structure of the representation matrix is enforced explicitly through BD regularization. In a truly unsupervised training environment, Robust $S^2$ConvSCN outperforms its baseline version by a significant amount for both seen and unseen data on four well-known datasets. Arguably, such an ablation study has not been reported before.

$\ell_0$-Motivated Low-Rank Sparse Subspace Clustering

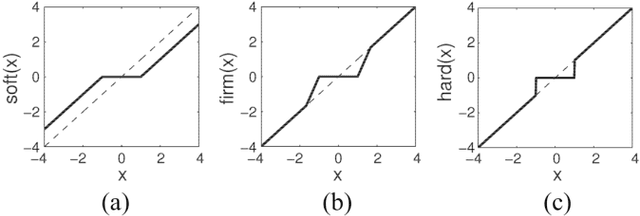
In many applications, high-dimensional data points can be well represented by low-dimensional subspaces. To identify the subspaces, it is important to capture a global and local structure of the data which is achieved by imposing low-rank and sparseness constraints on the data representation matrix. In low-rank sparse subspace clustering (LRSSC), nuclear and $\ell_1$ norms are used to measure rank and sparsity. However, the use of nuclear and $\ell_1$ norms leads to an overpenalized problem and only approximates the original problem. In this paper, we propose two $\ell_0$ quasi-norm based regularizations. First, the paper presents regularization based on multivariate generalization of minimax-concave penalty (GMC-LRSSC), which contains the global minimizers of $\ell_0$ quasi-norm regularized objective. Afterward, we introduce the Schatten-0 ($S_0$) and $\ell_0$ regularized objective and approximate the proximal map of the joint solution using a proximal average method ($S_0/\ell_0$-LRSSC). The resulting nonconvex optimization problems are solved using alternating direction method of multipliers with established convergence conditions of both algorithms. Results obtained on synthetic and four real-world datasets show the effectiveness of GMC-LRSSC and $S_0/\ell_0$-LRSSC when compared to state-of-the-art methods.