A Hyperspectral Imaging Dataset and Methodology for Intraoperative Pixel-Wise Classification of Metastatic Colon Cancer in the Liver

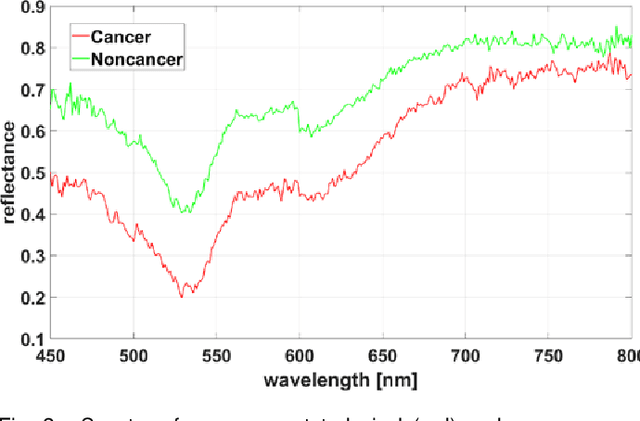
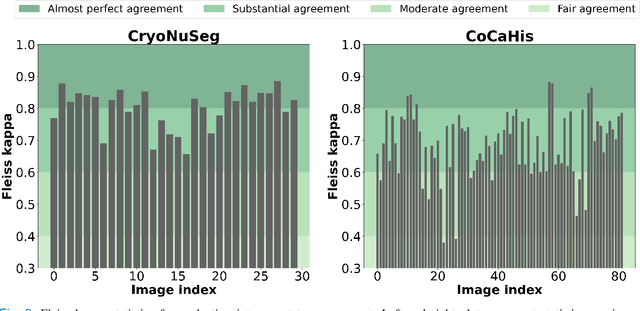
Hyperspectral imaging (HSI) holds significant potential for transforming the field of computational pathology. However, there is currently a shortage of pixel-wise annotated HSI data necessary for training deep learning (DL) models. Additionally, the number of HSI-based research studies remains limited, and in many cases, the advantages of HSI over traditional RGB imaging have not been conclusively demonstrated, particularly for specimens collected intraoperatively. To address these challenges we present a database consisted of 27 HSIs of hematoxylin-eosin stained frozen sections, collected from 14 patients with colon adenocarcinoma metastasized to the liver. It is aimed to validate pixel-wise classification for intraoperative tumor resection. The HSIs were acquired in the spectral range of 450 to 800 nm, with a resolution of 1 nm, resulting in images of 1384x1035 pixels. Pixel-wise annotations were performed by three pathologists. To overcome challenges such as experimental variability and the lack of annotated data, we combined label-propagation-based semi-supervised learning (SSL) with spectral-spatial features extracted by: the multiscale principle of relevant information (MPRI) method and tensor singular spectrum analysis method. Using only 1% of labeled pixels per class the SSL-MPRI method achieved a micro balanced accuracy (BACC) of 0.9313 and a micro F1-score of 0.9235 on the HSI dataset. The performance on corresponding RGB images was lower, with a micro BACC of 0.8809 and a micro F1-score of 0.8688. These improvements are statistically significant. The SSL-MPRI approach outperformed six DL architectures trained with 63% of labeled pixels. Data and code are available at: https://github.com/ikopriva/ColonCancerHSI.

LEFM-Nets: Learnable Explicit Feature Map Deep Networks for Segmentation of Histopathological Images of Frozen Sections

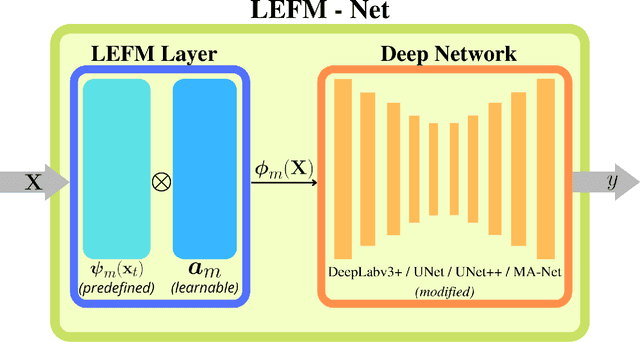
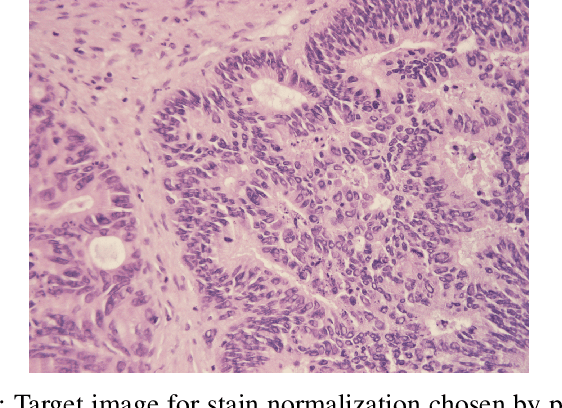
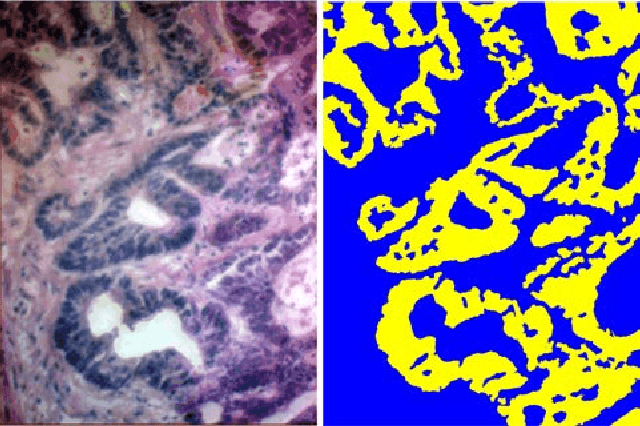
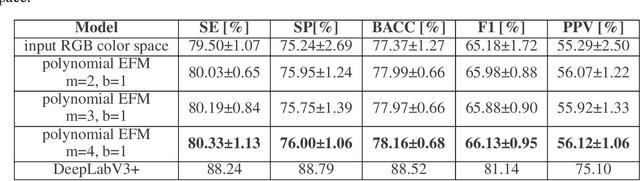
Accurate segmentation of medical images is essential for diagnosis and treatment of diseases. These problems are solved by highly complex models, such as deep networks (DN), requiring a large amount of labeled data for training. Thereby, many DNs possess task- or imaging modality specific architectures with a decision-making process that is often hard to explain and interpret. Here, we propose a framework that embeds existing DNs into a low-dimensional subspace induced by the learnable explicit feature map (LEFM) layer. Compared to the existing DN, the framework adds one hyperparameter and only modestly increase the number of learnable parameters. The method is aimed at, but not limited to, segmentation of low-dimensional medical images, such as color histopathological images of stained frozen sections. Since features in the LEFM layer are polynomial functions of the original features, proposed LEFM-Nets contribute to the interpretability of network decisions. In this work, we combined LEFM with the known networks: DeepLabv3+, UNet, UNet++ and MA-net. New LEFM-Nets are applied to the segmentation of adenocarcinoma of a colon in a liver from images of hematoxylin and eosin (H&E) stained frozen sections. LEFM-Nets are also tested on nuclei segmentation from images of H&E stained frozen sections of ten human organs. On the first problem, LEFM-Nets achieved statistically significant performance improvement in terms of micro balanced accuracy and $F_1$ score than original networks. LEFM-Nets achieved only better performance in comparison with the original networks on the second problem. The source code is available at https://github.com/dsitnik/lefm.

Clustering and classification of low-dimensional data in explicit feature map domain: intraoperative pixel-wise diagnosis of adenocarcinoma of a colon in a liver

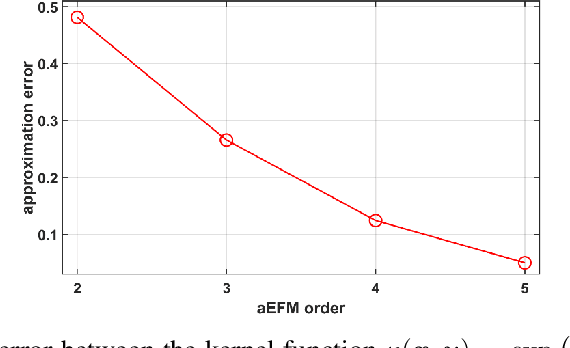
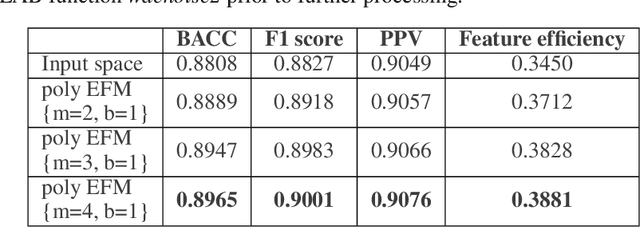
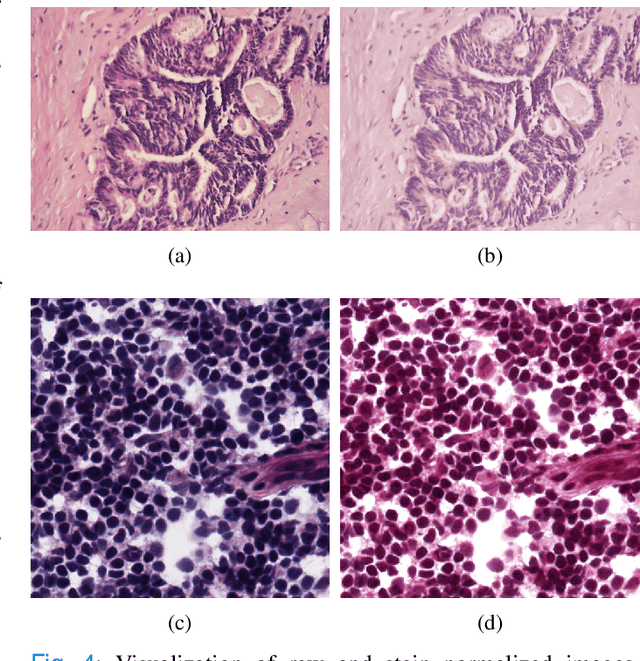
Application of artificial intelligence in medicine brings in highly accurate predictions achieved by complex models, the reasoning of which is hard to interpret. Their generalization ability can be reduced because of the lack of pixel wise annotated images that occurs in frozen section tissue analysis. To partially overcome this gap, this paper explores the approximate explicit feature map (aEFM) transform of low-dimensional data into a low-dimensional subspace in Hilbert space. There, with a modest increase in computational complexity, linear algorithms yield improved performance and keep interpretability. They remain amenable to incremental learning that is not a trivial issue for some nonlinear algorithms. We demonstrate proposed methodology on a very large-scale problem related to intraoperative pixel-wise semantic segmentation and clustering of adenocarcinoma of a colon in a liver. Compared to the results in the input space, logistic classifier achieved statistically significant performance improvements in micro balanced accuracy and F1 score in the amounts of 12.04% and 12.58%, respectively. Support vector machine classifier yielded the increase of 8.04% and 9.41%. For clustering, increases of 0.79% and 0.85% are obtained with ultra large-scale spectral clustering algorithm. Results are supported by a discussion of interpretability using Shapely additive explanation values for predictions of linear classifier in input space and aEFM induced space.

Robust Self-Supervised Convolutional Neural Network for Subspace Clustering and Classification

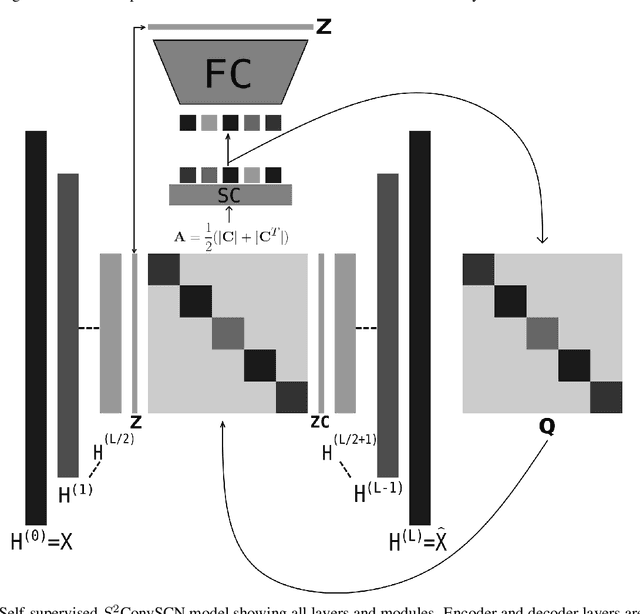
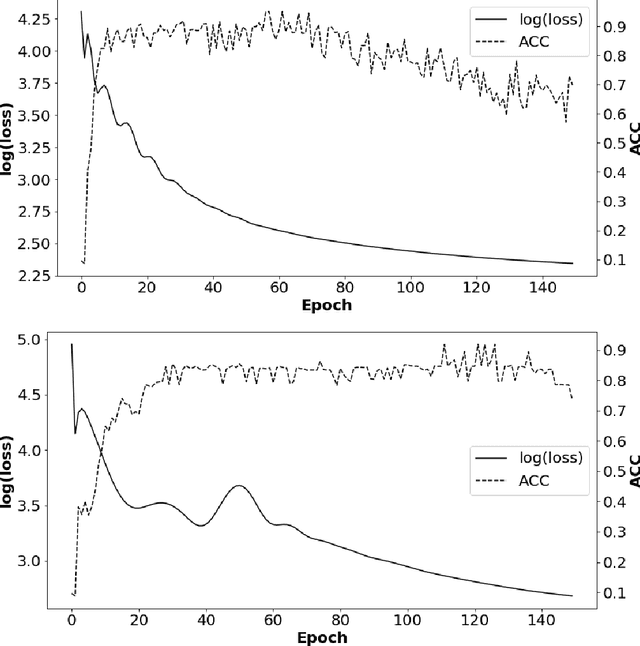
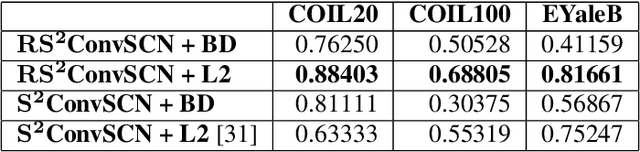
Insufficient capability of existing subspace clustering methods to handle data coming from nonlinear manifolds, data corruptions, and out-of-sample data hinders their applicability to address real-world clustering and classification problems. This paper proposes the robust formulation of the self-supervised convolutional subspace clustering network ($S^2$ConvSCN) that incorporates the fully connected (FC) layer and, thus, it is capable for handling out-of-sample data by classifying them using a softmax classifier. $S^2$ConvSCN clusters data coming from nonlinear manifolds by learning the linear self-representation model in the feature space. Robustness to data corruptions is achieved by using the correntropy induced metric (CIM) of the error. Furthermore, the block-diagonal (BD) structure of the representation matrix is enforced explicitly through BD regularization. In a truly unsupervised training environment, Robust $S^2$ConvSCN outperforms its baseline version by a significant amount for both seen and unseen data on four well-known datasets. Arguably, such an ablation study has not been reported before.