Robust Self-Supervised Convolutional Neural Network for Subspace Clustering and Classification
Paper and Code
Apr 03, 2020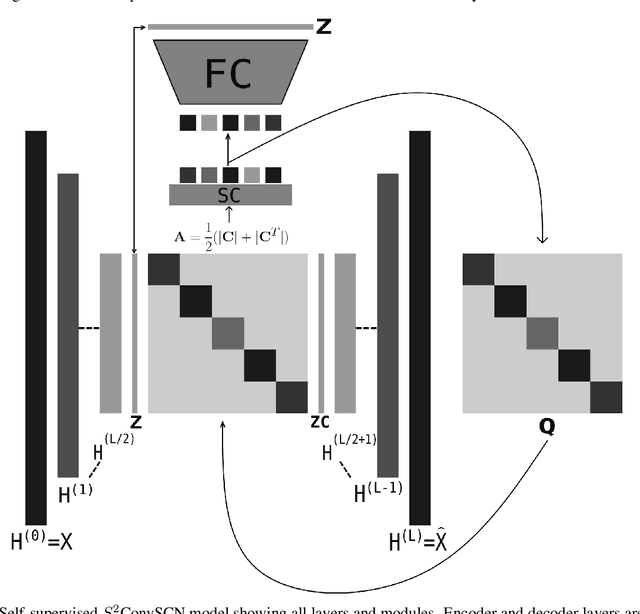
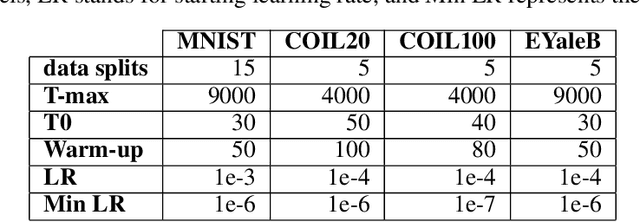
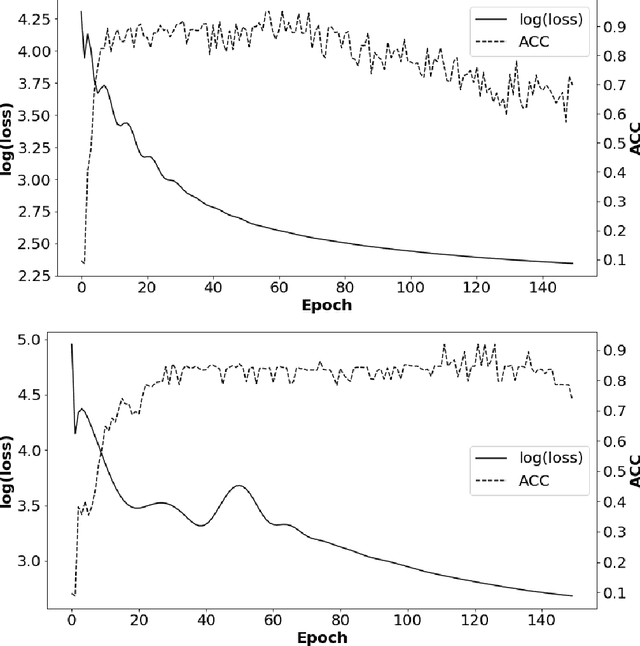
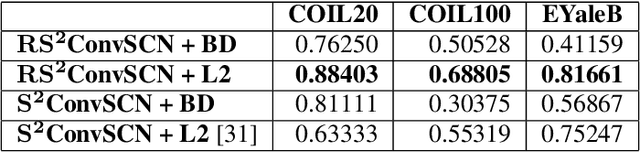
Insufficient capability of existing subspace clustering methods to handle data coming from nonlinear manifolds, data corruptions, and out-of-sample data hinders their applicability to address real-world clustering and classification problems. This paper proposes the robust formulation of the self-supervised convolutional subspace clustering network ($S^2$ConvSCN) that incorporates the fully connected (FC) layer and, thus, it is capable for handling out-of-sample data by classifying them using a softmax classifier. $S^2$ConvSCN clusters data coming from nonlinear manifolds by learning the linear self-representation model in the feature space. Robustness to data corruptions is achieved by using the correntropy induced metric (CIM) of the error. Furthermore, the block-diagonal (BD) structure of the representation matrix is enforced explicitly through BD regularization. In a truly unsupervised training environment, Robust $S^2$ConvSCN outperforms its baseline version by a significant amount for both seen and unseen data on four well-known datasets. Arguably, such an ablation study has not been reported before.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge