$\ell_0$-Motivated Low-Rank Sparse Subspace Clustering
Paper and Code
Dec 17, 2018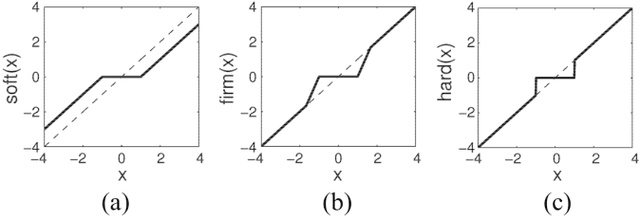
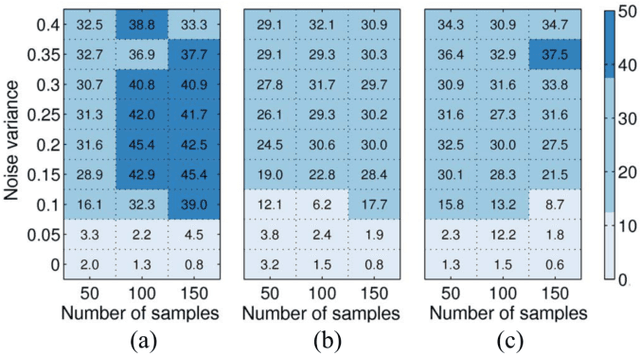
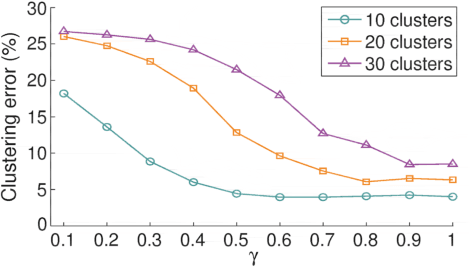

In many applications, high-dimensional data points can be well represented by low-dimensional subspaces. To identify the subspaces, it is important to capture a global and local structure of the data which is achieved by imposing low-rank and sparseness constraints on the data representation matrix. In low-rank sparse subspace clustering (LRSSC), nuclear and $\ell_1$ norms are used to measure rank and sparsity. However, the use of nuclear and $\ell_1$ norms leads to an overpenalized problem and only approximates the original problem. In this paper, we propose two $\ell_0$ quasi-norm based regularizations. First, the paper presents regularization based on multivariate generalization of minimax-concave penalty (GMC-LRSSC), which contains the global minimizers of $\ell_0$ quasi-norm regularized objective. Afterward, we introduce the Schatten-0 ($S_0$) and $\ell_0$ regularized objective and approximate the proximal map of the joint solution using a proximal average method ($S_0/\ell_0$-LRSSC). The resulting nonconvex optimization problems are solved using alternating direction method of multipliers with established convergence conditions of both algorithms. Results obtained on synthetic and four real-world datasets show the effectiveness of GMC-LRSSC and $S_0/\ell_0$-LRSSC when compared to state-of-the-art methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge