Trajectory optimization for contact-rich motions using implicit differential dynamic programming

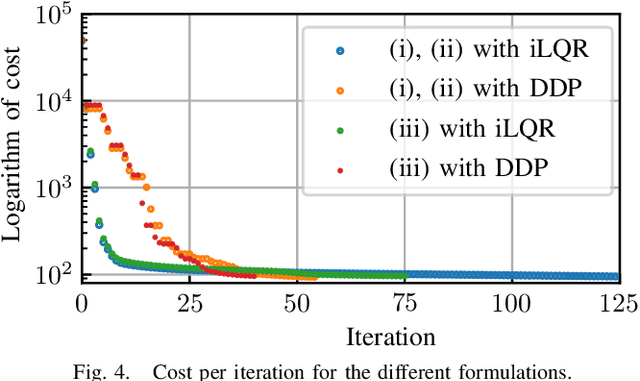
This paper presents a novel approach using sensitivity analysis for generalizing Differential Dynamic Programming (DDP) to systems characterized by implicit dynamics, such as those modelled via inverse dynamics and variational or implicit integrators. It leads to a more general formulation of DDP, enabling for example the use of the faster recursive Newton-Euler inverse dynamics. We leverage the implicit formulation for precise and exact contact modelling in DDP, where we focus on two contributions: (1) Contact dynamics in acceleration level that enables high-order integration schemes; (2) Formulation using an invertible contact model in the forward pass and a closed form solution in the backward pass to improve the numerical resolution of contacts. The performance of the proposed framework is validated (1) by comparing implicit versus explicit DDP for the swing-up of a double pendulum, and (2) by planning motions for two tasks using a single leg model making multi-body contacts with the environment: standing up from ground, where a priori contact enumeration is challenging, and maintaining balance under an external perturbation.

Contact-Implicit Trajectory Optimization using an Analytically Solvable Contact Model for Locomotion on Variable Ground

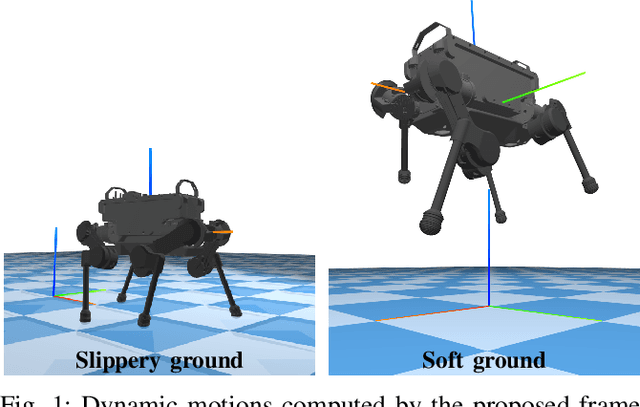
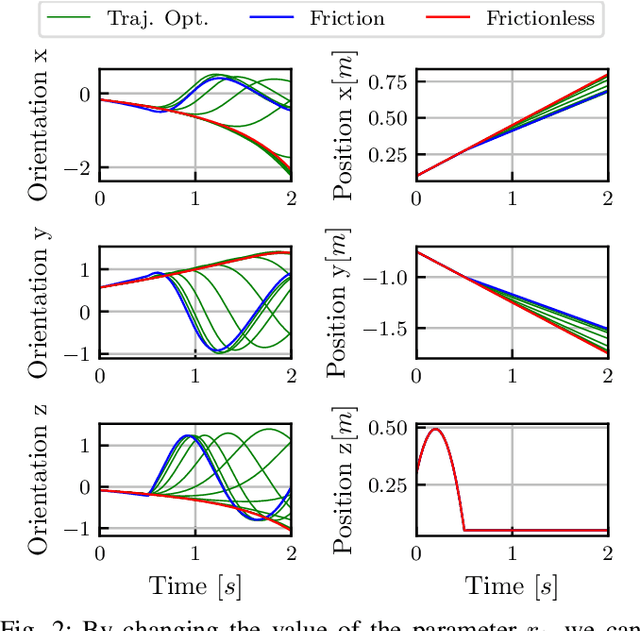
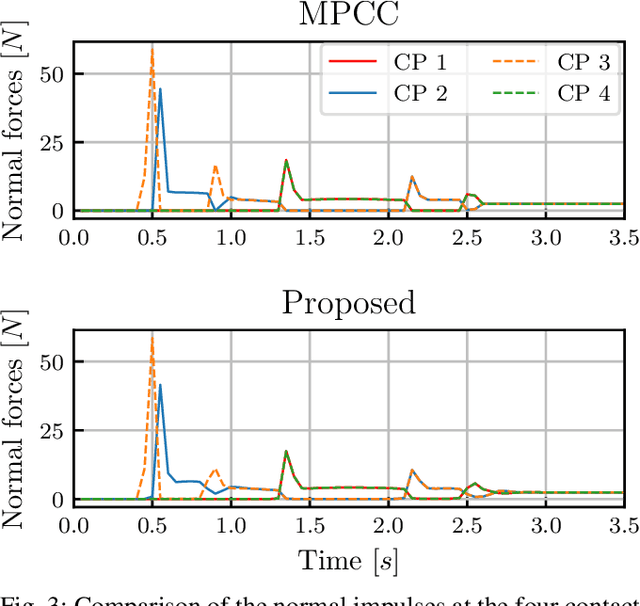
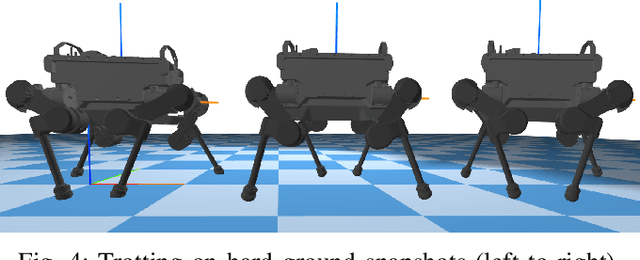
This paper presents a novel contact-implicit trajectory optimization method using an analytically solvable contact model to enable planning of interactions with hard, soft, and slippery environments. Specifically, we propose a novel contact model that can be computed in closed-form, satisfies friction cone constraints and can be embedded into direct trajectory optimization frameworks without complementarity constraints. The closed-form solution decouples the computation of the contact forces from other actuation forces and this property is used to formulate a minimal direct optimization problem expressed with configuration variables only. Our simulation study demonstrates the advantages over the rigid contact model and a trajectory optimization approach based on complementarity constraints. The proposed model enables physics-based optimization for a wide range of interactions with hard, slippery, and soft grounds in a unified manner expressed by two parameters only. By computing trotting and jumping motions for a quadruped robot, the proposed optimization demonstrates the versatility for multi-contact motion planning on surfaces with different physical properties.

Comparison Study of Nonlinear Optimization of Step Durations and Foot Placement for Dynamic Walking

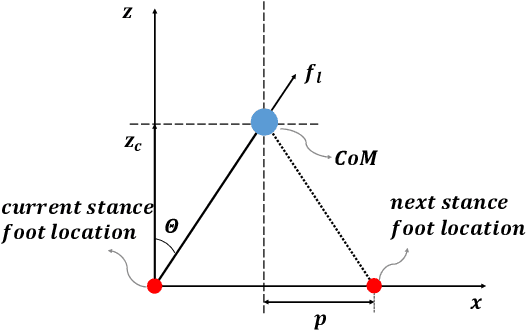
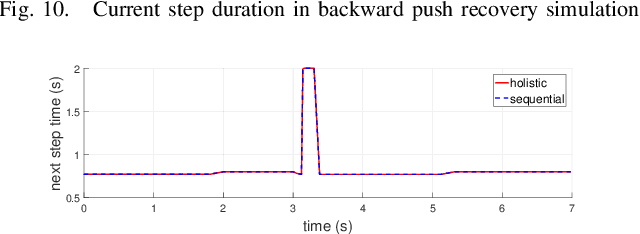
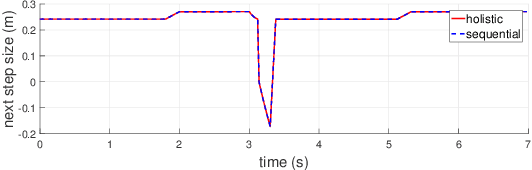
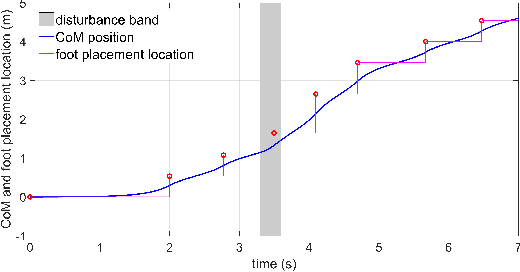
This paper studies bipedal locomotion as a nonlinear optimization problem based on continuous and discrete dynamics, by simultaneously optimizing the remaining step duration, the next step duration and the foot location to achieve robustness. The linear inverted pendulum as the motion model captures the center of mass dynamics and its low-dimensionality makes the problem more tractable. We first formulate a holistic approach to search for optimality in the three-dimensional parametric space and use these results as baseline. To further improve computational efficiency, our study investigates a sequential approach with two stages of customized optimization that first optimizes the current step duration, and subsequently the duration and location of the next step. The effectiveness of both approaches is successfully demonstrated in simulation by applying different perturbations. The comparison study shows that these two approaches find mostly the same optimal solutions, but the latter requires considerably less computational time, which suggests that the proposed sequential approach is well suited for real-time implementation with a minor trade-off in optimality.