Comparison Study of Nonlinear Optimization of Step Durations and Foot Placement for Dynamic Walking
Paper and Code
May 06, 2018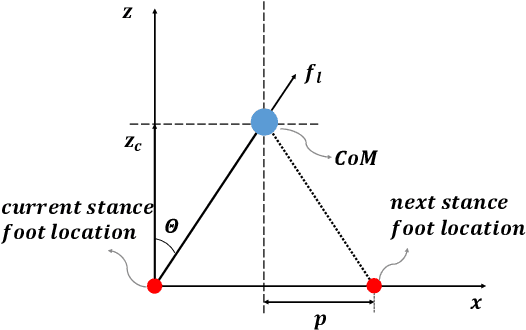
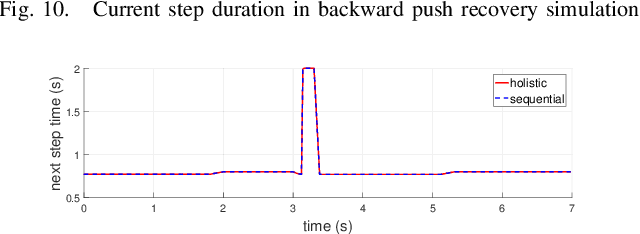
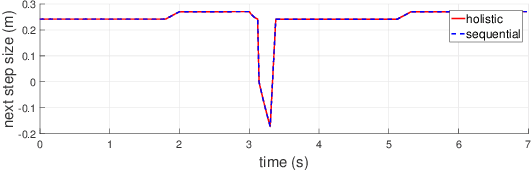
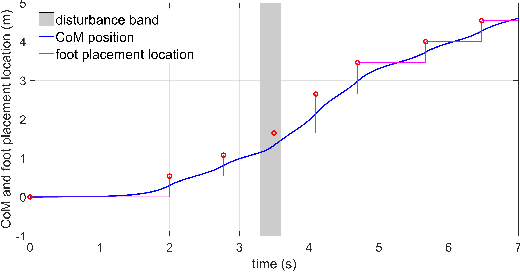
This paper studies bipedal locomotion as a nonlinear optimization problem based on continuous and discrete dynamics, by simultaneously optimizing the remaining step duration, the next step duration and the foot location to achieve robustness. The linear inverted pendulum as the motion model captures the center of mass dynamics and its low-dimensionality makes the problem more tractable. We first formulate a holistic approach to search for optimality in the three-dimensional parametric space and use these results as baseline. To further improve computational efficiency, our study investigates a sequential approach with two stages of customized optimization that first optimizes the current step duration, and subsequently the duration and location of the next step. The effectiveness of both approaches is successfully demonstrated in simulation by applying different perturbations. The comparison study shows that these two approaches find mostly the same optimal solutions, but the latter requires considerably less computational time, which suggests that the proposed sequential approach is well suited for real-time implementation with a minor trade-off in optimality.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge