Coordinate-based neural representations for computational adaptive optics in widefield microscopy

Widefield microscopy is widely used for non-invasive imaging of biological structures at subcellular resolution. When applied to complex specimen, its image quality is degraded by sample-induced optical aberration. Adaptive optics can correct wavefront distortion and restore diffraction-limited resolution but require wavefront sensing and corrective devices, increasing system complexity and cost. Here, we describe a self-supervised machine learning algorithm, CoCoA, that performs joint wavefront estimation and three-dimensional structural information extraction from a single input 3D image stack without the need for external training dataset. We implemented CoCoA for widefield imaging of mouse brain tissues and validated its performance with direct-wavefront-sensing-based adaptive optics. Importantly, we systematically explored and quantitatively characterized the limiting factors of CoCoA's performance. Using CoCoA, we demonstrated the first in vivo widefield mouse brain imaging using machine-learning-based adaptive optics. Incorporating coordinate-based neural representations and a forward physics model, the self-supervised scheme of CoCoA should be applicable to microscopy modalities in general.

Accelerated deep self-supervised ptycho-laminography for three-dimensional nanoscale imaging of integrated circuits

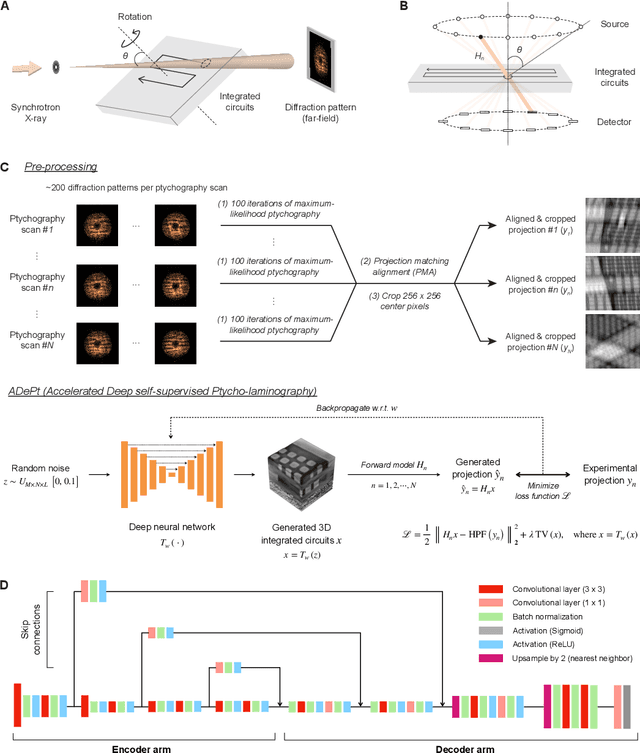
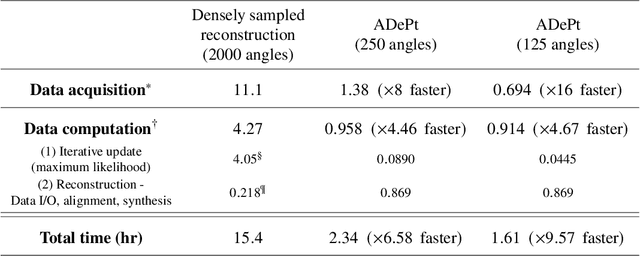
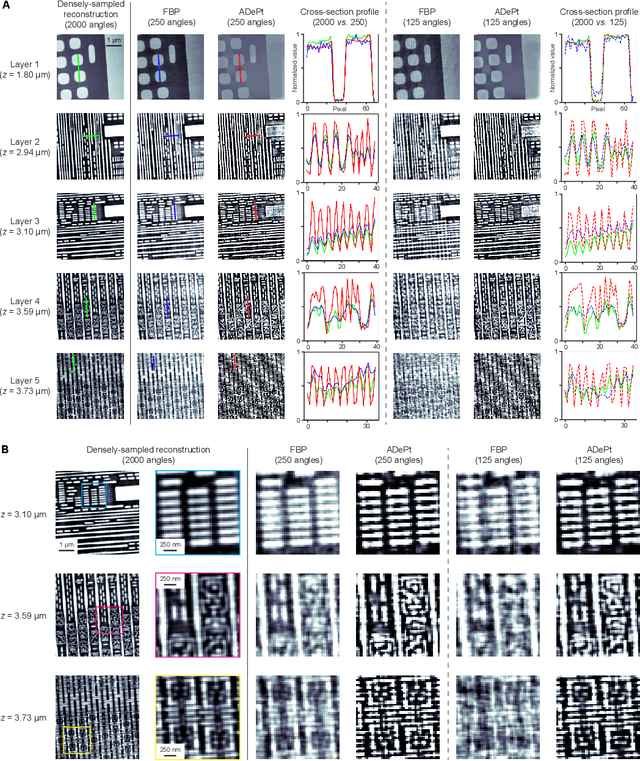
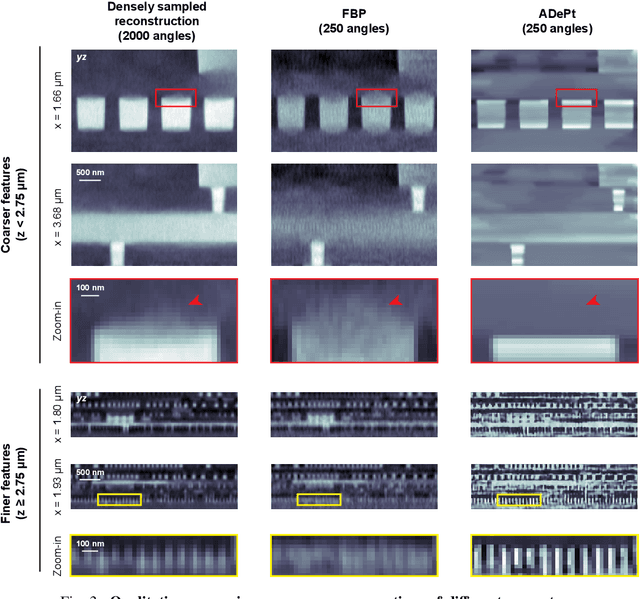
Three-dimensional inspection of nanostructures such as integrated circuits is important for security and reliability assurance. Two scanning operations are required: ptychographic to recover the complex transmissivity of the specimen; and rotation of the specimen to acquire multiple projections covering the 3D spatial frequency domain. Two types of rotational scanning are possible: tomographic and laminographic. For flat, extended samples, for which the full 180 degree coverage is not possible, the latter is preferable because it provides better coverage of the 3D spatial frequency domain compared to limited-angle tomography. It is also because the amount of attenuation through the sample is approximately the same for all projections. However, both techniques are time consuming because of extensive acquisition and computation time. Here, we demonstrate the acceleration of ptycho-laminographic reconstruction of integrated circuits with 16-times fewer angular samples and 4.67-times faster computation by using a physics-regularized deep self-supervised learning architecture. We check the fidelity of our reconstruction against a densely sampled reconstruction that uses full scanning and no learning. As already reported elsewhere [Zhou and Horstmeyer, Opt. Express, 28(9), pp. 12872-12896], we observe improvement of reconstruction quality even over the densely sampled reconstruction, due to the ability of the self-supervised learning kernel to fill the missing cone.

Attentional Ptycho-Tomography (APT) for three-dimensional nanoscale X-ray imaging with minimal data acquisition and computation time

Noninvasive X-ray imaging of nanoscale three-dimensional objects, e.g. integrated circuits (ICs), generally requires two types of scanning: ptychographic, which is translational and returns estimates of complex electromagnetic field through ICs; and tomographic scanning, which collects complex field projections from multiple angles. Here, we present Attentional Ptycho-Tomography (APT), an approach trained to provide accurate reconstructions of ICs despite incomplete measurements, using a dramatically reduced amount of angular scanning. Training process includes regularizing priors based on typical IC patterns and the physics of X-ray propagation. We demonstrate that APT with 12-time reduced angles achieves fidelity comparable to the gold standard with the original set of angles. With the same set of reduced angles, APT also outperforms baseline reconstruction methods. In our experiments, APT achieves 108-time aggregate reduction in data acquisition and computation without compromising quality. We expect our physics-assisted machine learning framework could also be applied to other branches of nanoscale imaging.

Limited-angle tomographic reconstruction of dense layered objects by dynamical machine learning

Limited-angle tomography of strongly scattering quasi-transparent objects is a challenging, highly ill-posed problem with practical implications in medical and biological imaging, manufacturing, automation, and environmental and food security. Regularizing priors are necessary to reduce artifacts by improving the condition of such problems. Recently, it was shown that one effective way to learn the priors for strongly scattering yet highly structured 3D objects, e.g. layered and Manhattan, is by a static neural network [Goy et al, Proc. Natl. Acad. Sci. 116, 19848-19856 (2019)]. Here, we present a radically different approach where the collection of raw images from multiple angles is viewed analogously to a dynamical system driven by the object-dependent forward scattering operator. The sequence index in angle of illumination plays the role of discrete time in the dynamical system analogy. Thus, the imaging problem turns into a problem of nonlinear system identification, which also suggests dynamical learning as better fit to regularize the reconstructions. We devised a recurrent neural network (RNN) architecture with a novel split-convolutional gated recurrent unit (SC-GRU) as the fundamental building block. Through comprehensive comparison of several quantitative metrics, we show that the dynamic method improves upon previous static approaches with fewer artifacts and better overall reconstruction fidelity.

On the interplay between physical and content priors in deep learning for computational imaging

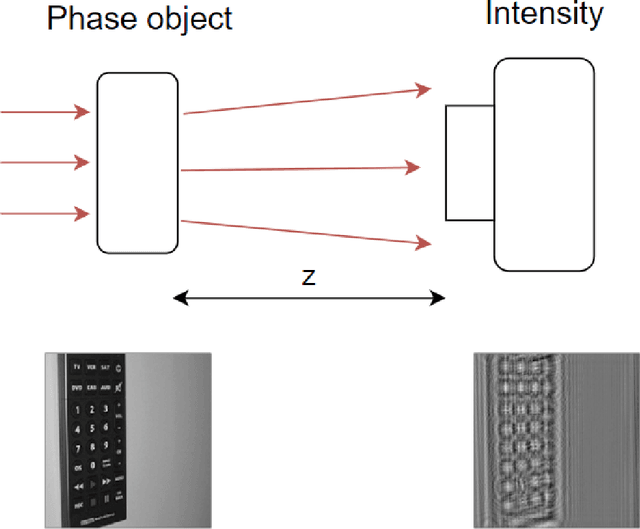
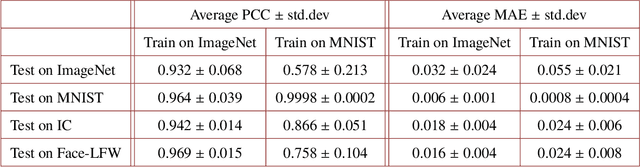
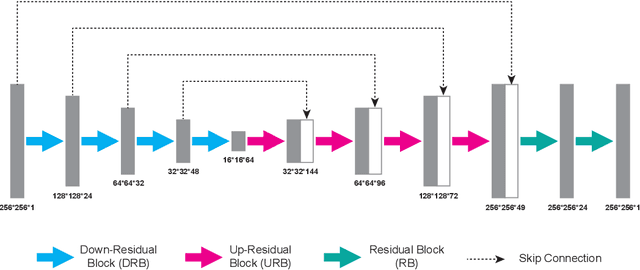
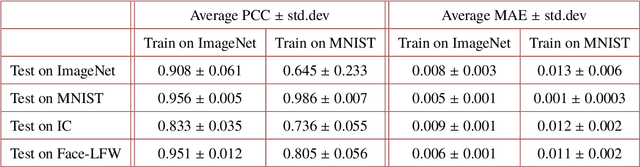
Deep learning (DL) has been applied extensively in many computational imaging problems, often leading to superior performance over traditional iterative approaches. However, two important questions remain largely unanswered: first, how well can the trained neural network generalize to objects very different from the ones in training? This is particularly important in practice, since large-scale annotated examples similar to those of interest are often not available during training. Second, has the trained neural network learnt the underlying (inverse) physics model, or has it merely done something trivial, such as memorizing the examples or point-wise pattern matching? This pertains to the interpretability of machine-learning based algorithms. In this work, we use the Phase Extraction Neural Network (PhENN), a deep neural network (DNN) for quantitative phase retrieval in a lensless phase imaging system as the standard platform and show that the two questions are related and share a common crux: the choice of the training examples. Moreover, we connect the strength of the regularization effect imposed by a training set to the training process with the Shannon entropy of images in the dataset. That is, the higher the entropy of the training images, the weaker the regularization effect can be imposed. We also discover that weaker regularization effect leads to better learning of the underlying propagation model, i.e. the weak object transfer function, applicable for weakly scattering objects under the weak object approximation. Finally, simulation and experimental results show that better cross-domain generalization performance can be achieved if DNN is trained on a higher-entropy database, e.g. the ImageNet, than if the same DNN is trained on a lower-entropy database, e.g. MNIST, as the former allows the underlying physics model be learned better than the latter.

Learning to Synthesize: Robust Phase Retrieval at Low Photon counts

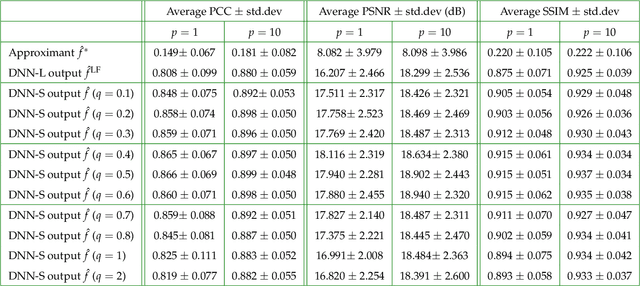
The quality of inverse problem solutions obtained through deep learning [Barbastathis et al, 2019] is limited by the nature of the priors learned from examples presented during the training phase. In the case of quantitative phase retrieval [Sinha et al, 2017, Goy et al, 2019], in particular, spatial frequencies that are underrepresented in the training database, most often at the high band, tend to be suppressed in the reconstruction. Ad hoc solutions have been proposed, such as pre-amplifying the high spatial frequencies in the examples [Li et al, 2018]; however, while that strategy improves resolution, it also leads to high-frequency artifacts as well as low-frequency distortions in the reconstructions. Here, we present a new approach that learns separately how to handle the two frequency bands, low and high; and also learns how to synthesize these two bands into the full-band reconstructions. We show that this "learning to synthesize" (LS) method yields phase reconstructions of high spatial resolution and artifact-free; and it is also resilient to high-noise conditions, e.g. in the case of very low photon flux. In addition to the problem of quantitative phase retrieval, the LS method is applicable, in principle, to any inverse problem where the forward operator treats different frequency bands unevenly, i.e. is ill-posed.