Limited-angle tomographic reconstruction of dense layered objects by dynamical machine learning

Limited-angle tomography of strongly scattering quasi-transparent objects is a challenging, highly ill-posed problem with practical implications in medical and biological imaging, manufacturing, automation, and environmental and food security. Regularizing priors are necessary to reduce artifacts by improving the condition of such problems. Recently, it was shown that one effective way to learn the priors for strongly scattering yet highly structured 3D objects, e.g. layered and Manhattan, is by a static neural network [Goy et al, Proc. Natl. Acad. Sci. 116, 19848-19856 (2019)]. Here, we present a radically different approach where the collection of raw images from multiple angles is viewed analogously to a dynamical system driven by the object-dependent forward scattering operator. The sequence index in angle of illumination plays the role of discrete time in the dynamical system analogy. Thus, the imaging problem turns into a problem of nonlinear system identification, which also suggests dynamical learning as better fit to regularize the reconstructions. We devised a recurrent neural network (RNN) architecture with a novel split-convolutional gated recurrent unit (SC-GRU) as the fundamental building block. Through comprehensive comparison of several quantitative metrics, we show that the dynamic method improves upon previous static approaches with fewer artifacts and better overall reconstruction fidelity.

Learning to Synthesize: Robust Phase Retrieval at Low Photon counts

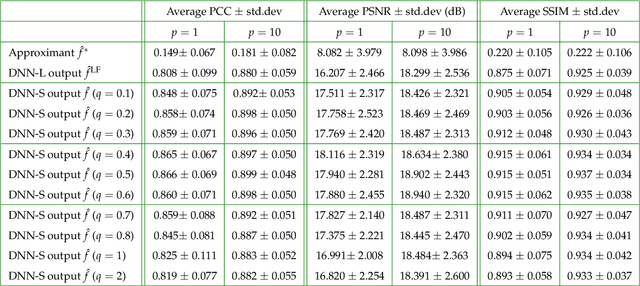
The quality of inverse problem solutions obtained through deep learning [Barbastathis et al, 2019] is limited by the nature of the priors learned from examples presented during the training phase. In the case of quantitative phase retrieval [Sinha et al, 2017, Goy et al, 2019], in particular, spatial frequencies that are underrepresented in the training database, most often at the high band, tend to be suppressed in the reconstruction. Ad hoc solutions have been proposed, such as pre-amplifying the high spatial frequencies in the examples [Li et al, 2018]; however, while that strategy improves resolution, it also leads to high-frequency artifacts as well as low-frequency distortions in the reconstructions. Here, we present a new approach that learns separately how to handle the two frequency bands, low and high; and also learns how to synthesize these two bands into the full-band reconstructions. We show that this "learning to synthesize" (LS) method yields phase reconstructions of high spatial resolution and artifact-free; and it is also resilient to high-noise conditions, e.g. in the case of very low photon flux. In addition to the problem of quantitative phase retrieval, the LS method is applicable, in principle, to any inverse problem where the forward operator treats different frequency bands unevenly, i.e. is ill-posed.