On the interplay between physical and content priors in deep learning for computational imaging

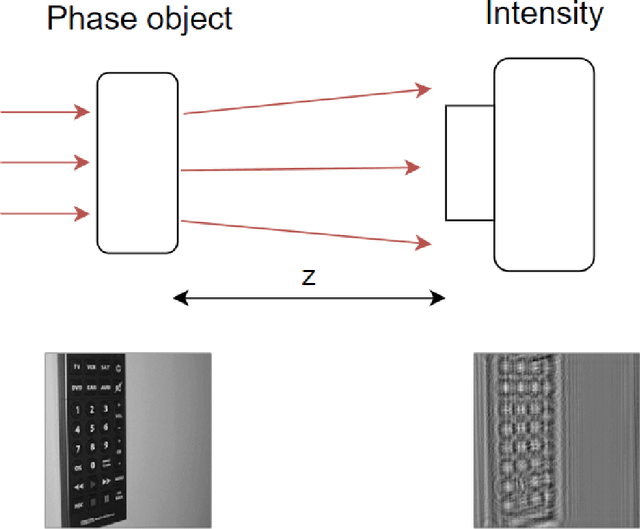
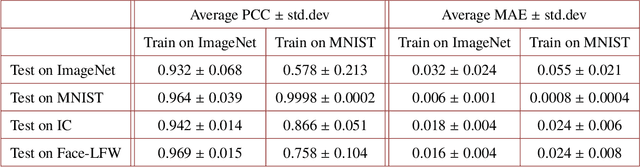
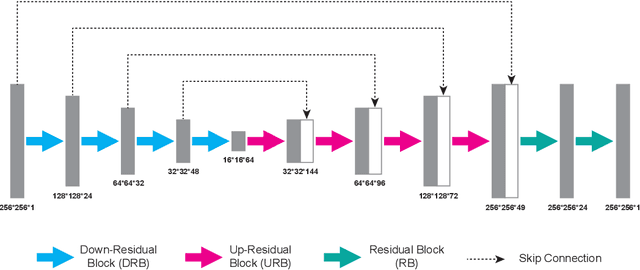
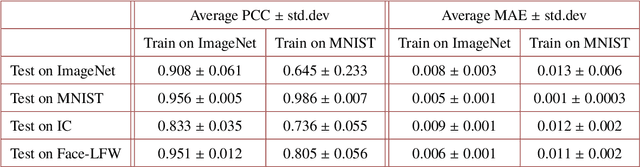
Deep learning (DL) has been applied extensively in many computational imaging problems, often leading to superior performance over traditional iterative approaches. However, two important questions remain largely unanswered: first, how well can the trained neural network generalize to objects very different from the ones in training? This is particularly important in practice, since large-scale annotated examples similar to those of interest are often not available during training. Second, has the trained neural network learnt the underlying (inverse) physics model, or has it merely done something trivial, such as memorizing the examples or point-wise pattern matching? This pertains to the interpretability of machine-learning based algorithms. In this work, we use the Phase Extraction Neural Network (PhENN), a deep neural network (DNN) for quantitative phase retrieval in a lensless phase imaging system as the standard platform and show that the two questions are related and share a common crux: the choice of the training examples. Moreover, we connect the strength of the regularization effect imposed by a training set to the training process with the Shannon entropy of images in the dataset. That is, the higher the entropy of the training images, the weaker the regularization effect can be imposed. We also discover that weaker regularization effect leads to better learning of the underlying propagation model, i.e. the weak object transfer function, applicable for weakly scattering objects under the weak object approximation. Finally, simulation and experimental results show that better cross-domain generalization performance can be achieved if DNN is trained on a higher-entropy database, e.g. the ImageNet, than if the same DNN is trained on a lower-entropy database, e.g. MNIST, as the former allows the underlying physics model be learned better than the latter.

Learning to Synthesize: Robust Phase Retrieval at Low Photon counts

The quality of inverse problem solutions obtained through deep learning [Barbastathis et al, 2019] is limited by the nature of the priors learned from examples presented during the training phase. In the case of quantitative phase retrieval [Sinha et al, 2017, Goy et al, 2019], in particular, spatial frequencies that are underrepresented in the training database, most often at the high band, tend to be suppressed in the reconstruction. Ad hoc solutions have been proposed, such as pre-amplifying the high spatial frequencies in the examples [Li et al, 2018]; however, while that strategy improves resolution, it also leads to high-frequency artifacts as well as low-frequency distortions in the reconstructions. Here, we present a new approach that learns separately how to handle the two frequency bands, low and high; and also learns how to synthesize these two bands into the full-band reconstructions. We show that this "learning to synthesize" (LS) method yields phase reconstructions of high spatial resolution and artifact-free; and it is also resilient to high-noise conditions, e.g. in the case of very low photon flux. In addition to the problem of quantitative phase retrieval, the LS method is applicable, in principle, to any inverse problem where the forward operator treats different frequency bands unevenly, i.e. is ill-posed.

Learning to synthesize: splitting and recombining low and high spatial frequencies for image recovery

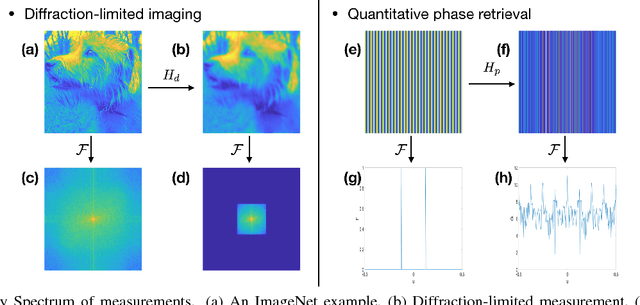
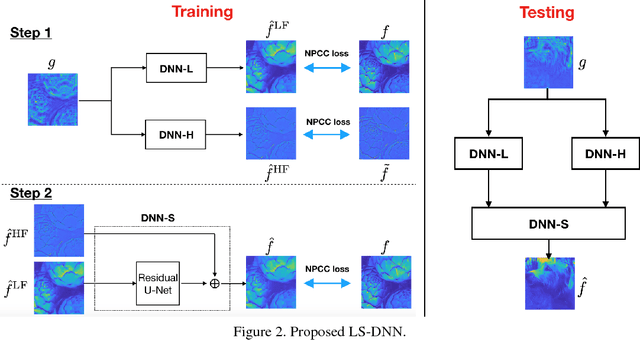
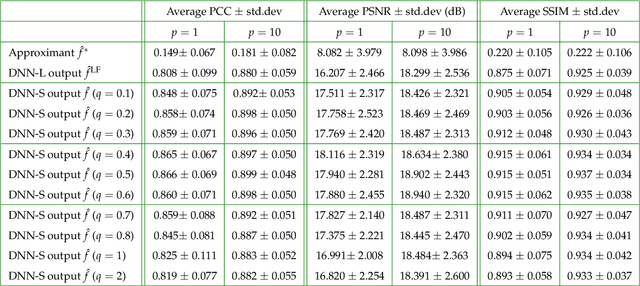
Deep Neural Network (DNN)-based image reconstruction, despite many successes, often exhibits uneven fidelity between high and low spatial frequency bands. In this paper we propose the Learning Synthesis by DNN (LS-DNN) approach where two DNNs process the low and high spatial frequencies, respectively, and, improving over [30], the two DNNs are trained separately and a third DNN combines them into an image with high fidelity at all bands. We demonstrate LS-DNN in two canonical inverse problems: super-resolution (SR) in diffraction-limited imaging (DLI), and quantitative phase retrieval (QPR). Our results also show comparable or improved performance over perceptual-loss based SR [21], and can be generalized to a wider range of image recovery problems.