Newton-PnP: Real-time Visual Navigation for Autonomous Toy-Drones

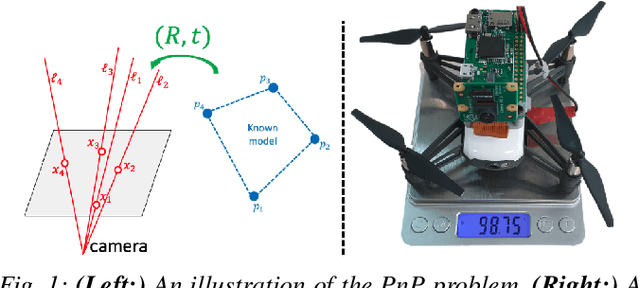
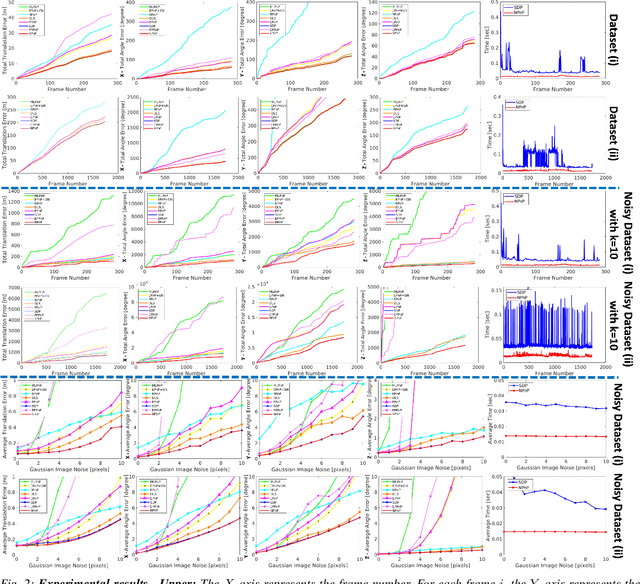
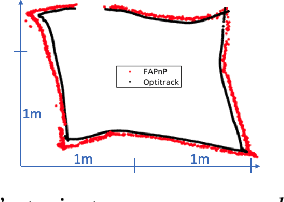
The Perspective-n-Point problem aims to estimate the relative pose between a calibrated monocular camera and a known 3D model, by aligning pairs of 2D captured image points to their corresponding 3D points in the model. We suggest an algorithm that runs on weak IoT devices in real-time but still provides provable theoretical guarantees for both running time and correctness. Existing solvers provide only one of these requirements. Our main motivation was to turn the popular DJI's Tello Drone (<90gr, <\$100) into an autonomous drone that navigates in an indoor environment with no external human/laptop/sensor, by simply attaching a Raspberry PI Zero (<9gr, <\$25) to it. This tiny micro-processor takes as input a real-time video from a tiny RGB camera, and runs our PnP solver on-board. Extensive experimental results, open source code, and a demonstration video are included.

Introduction to Coresets: Approximated Mean

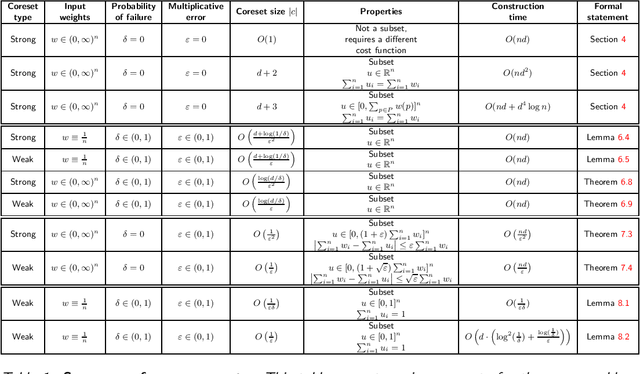
A \emph{strong coreset} for the mean queries of a set $P$ in ${\mathbb{R}}^d$ is a small weighted subset $C\subseteq P$, which provably approximates its sum of squared distances to any center (point) $x\in {\mathbb{R}}^d$. A \emph{weak coreset} is (also) a small weighted subset $C$ of $P$, whose mean approximates the mean of $P$. While computing the mean of $P$ can be easily computed in linear time, its coreset can be used to solve harder constrained version, and is in the heart of generalizations such as coresets for $k$-means clustering. In this paper, we survey most of the mean coreset construction techniques, and suggest a unified analysis methodology for providing and explaining classical and modern results including step-by-step proofs. In particular, we collected folklore and scattered related results, some of which are not formally stated elsewhere. Throughout this survey, we present, explain, and prove a set of techniques, reductions, and algorithms very widespread and crucial in this field. However, when put to use in the (relatively simple) mean problem, such techniques are much simpler to grasp. The survey may help guide new researchers unfamiliar with the field, and introduce them to the very basic foundations of coresets, through a simple, yet fundamental, problem. Experts in this area might appreciate the unified analysis flow, and the comparison table for existing results. Finally, to encourage and help practitioners and software engineers, we provide full open source code for all presented algorithms.

Unsupervised High-Fidelity Facial Texture Generation and Reconstruction

Many methods have been proposed over the years to tackle the task of facial 3D geometry and texture recovery from a single image. Such methods often fail to provide high-fidelity texture without relying on 3D facial scans during training. In contrast, the complementary task of 3D facial generation has not received as much attention. As opposed to the 2D texture domain, where GANs have proven to produce highly realistic facial images, the more challenging 3D geometry domain has not yet caught up to the same levels of realism and diversity. In this paper, we propose a novel unified pipeline for both tasks, generation of both geometry and texture, and recovery of high-fidelity texture. Our texture model is learned, in an unsupervised fashion, from natural images as opposed to scanned texture maps. To the best of our knowledge, this is the first such unified framework independent of scanned textures. Our novel training pipeline incorporates a pre-trained 2D facial generator coupled with a deep feature manipulation methodology. By applying precise 3DMM fitting, we can seamlessly integrate our modeled textures into synthetically generated background images forming a realistic composition of our textured model with background, hair, teeth, and body. This enables us to apply transfer learning from the domain of 2D image generation, thus, benefiting greatly from the impressive results obtained in this domain. We provide a comprehensive study on several recent methods comparing our model in generation and reconstruction tasks. As the extensive qualitative, as well as quantitative analysis, demonstrate, we achieve state-of-the-art results for both tasks.

Coresets for Decision Trees of Signals

A $k$-decision tree $t$ (or $k$-tree) is a recursive partition of a matrix (2D-signal) into $k\geq 1$ block matrices (axis-parallel rectangles, leaves) where each rectangle is assigned a real label. Its regression or classification loss to a given matrix $D$ of $N$ entries (labels) is the sum of squared differences over every label in $D$ and its assigned label by $t$. Given an error parameter $\varepsilon\in(0,1)$, a $(k,\varepsilon)$-coreset $C$ of $D$ is a small summarization that provably approximates this loss to \emph{every} such tree, up to a multiplicative factor of $1\pm\varepsilon$. In particular, the optimal $k$-tree of $C$ is a $(1+\varepsilon)$-approximation to the optimal $k$-tree of $D$. We provide the first algorithm that outputs such a $(k,\varepsilon)$-coreset for \emph{every} such matrix $D$. The size $|C|$ of the coreset is polynomial in $k\log(N)/\varepsilon$, and its construction takes $O(Nk)$ time. This is by forging a link between decision trees from machine learning -- to partition trees in computational geometry. Experimental results on \texttt{sklearn} and \texttt{lightGBM} show that applying our coresets on real-world data-sets boosts the computation time of random forests and their parameter tuning by up to x$10$, while keeping similar accuracy. Full open source code is provided.

Provably Approximated ICP

The goal of the \emph{alignment problem} is to align a (given) point cloud $P = \{p_1,\cdots,p_n\}$ to another (observed) point cloud $Q = \{q_1,\cdots,q_n\}$. That is, to compute a rotation matrix $R \in \mathbb{R}^{3 \times 3}$ and a translation vector $t \in \mathbb{R}^{3}$ that minimize the sum of paired distances $\sum_{i=1}^n D(Rp_i-t,q_i)$ for some distance function $D$. A harder version is the \emph{registration problem}, where the correspondence is unknown, and the minimum is also over all possible correspondence functions from $P$ to $Q$. Heuristics such as the Iterative Closest Point (ICP) algorithm and its variants were suggested for these problems, but none yield a provable non-trivial approximation for the global optimum. We prove that there \emph{always} exists a "witness" set of $3$ pairs in $P \times Q$ that, via novel alignment algorithm, defines a constant factor approximation (in the worst case) to this global optimum. We then provide algorithms that recover this witness set and yield the first provable constant factor approximation for the: (i) alignment problem in $O(n)$ expected time, and (ii) registration problem in polynomial time. Such small witness sets exist for many variants including points in $d$-dimensional space, outlier-resistant cost functions, and different correspondence types. Extensive experimental results on real and synthetic datasets show that our approximation constants are, in practice, close to $1$, and up to x$10$ times smaller than state-of-the-art algorithms.

Faster PAC Learning and Smaller Coresets via Smoothed Analysis

PAC-learning usually aims to compute a small subset ($\varepsilon$-sample/net) from $n$ items, that provably approximates a given loss function for every query (model, classifier, hypothesis) from a given set of queries, up to an additive error $\varepsilon\in(0,1)$. Coresets generalize this idea to support multiplicative error $1\pm\varepsilon$. Inspired by smoothed analysis, we suggest a natural generalization: approximate the \emph{average} (instead of the worst-case) error over the queries, in the hope of getting smaller subsets. The dependency between errors of different queries implies that we may no longer apply the Chernoff-Hoeffding inequality for a fixed query, and then use the VC-dimension or union bound. This paper provides deterministic and randomized algorithms for computing such coresets and $\varepsilon$-samples of size independent of $n$, for any finite set of queries and loss function. Example applications include new and improved coreset constructions for e.g. streaming vector summarization [ICML'17] and $k$-PCA [NIPS'16]. Experimental results with open source code are provided.

Sets Clustering

The input to the \emph{sets-$k$-means} problem is an integer $k\geq 1$ and a set $\mathcal{P}=\{P_1,\cdots,P_n\}$ of sets in $\mathbb{R}^d$. The goal is to compute a set $C$ of $k$ centers (points) in $\mathbb{R}^d$ that minimizes the sum $\sum_{P\in \mathcal{P}} \min_{p\in P, c\in C}\left\| p-c \right\|^2$ of squared distances to these sets. An \emph{$\varepsilon$-core-set} for this problem is a weighted subset of $\mathcal{P}$ that approximates this sum up to $1\pm\varepsilon$ factor, for \emph{every} set $C$ of $k$ centers in $\mathbb{R}^d$. We prove that such a core-set of $O(\log^2{n})$ sets always exists, and can be computed in $O(n\log{n})$ time, for every input $\mathcal{P}$ and every fixed $d,k\geq 1$ and $\varepsilon \in (0,1)$. The result easily generalized for any metric space, distances to the power of $z>0$, and M-estimators that handle outliers. Applying an inefficient but optimal algorithm on this coreset allows us to obtain the first PTAS ($1+\varepsilon$ approximation) for the sets-$k$-means problem that takes time near linear in $n$. This is the first result even for sets-mean on the plane ($k=1$, $d=2$). Open source code and experimental results for document classification and facility locations are also provided.

Introduction to Coresets: Accurate Coresets

A coreset (or core-set) of an input set is its small summation, such that solving a problem on the coreset as its input, provably yields the same result as solving the same problem on the original (full) set, for a given family of problems (models, classifiers, loss functions). Over the past decade, coreset construction algorithms have been suggested for many fundamental problems in e.g. machine/deep learning, computer vision, graphics, databases, and theoretical computer science. This introductory paper was written following requests from (usually non-expert, but also colleagues) regarding the many inconsistent coreset definitions, lack of available source code, the required deep theoretical background from different fields, and the dense papers that make it hard for beginners to apply coresets and develop new ones. The paper provides folklore, classic and simple results including step-by-step proofs and figures, for the simplest (accurate) coresets of very basic problems, such as: sum of vectors, minimum enclosing ball, SVD/ PCA and linear regression. Nevertheless, we did not find most of their constructions in the literature. Moreover, we expect that putting them together in a retrospective context would help the reader to grasp modern results that usually extend and generalize these fundamental observations. Experts might appreciate the unified notation and comparison table that links between existing results. Open source code with example scripts are provided for all the presented algorithms, to demonstrate their practical usage, and to support the readers who are more familiar with programming than math.

Fast and Accurate Least-Mean-Squares Solvers

Least-mean squares (LMS) solvers such as Linear / Ridge / Lasso-Regression, SVD and Elastic-Net not only solve fundamental machine learning problems, but are also the building blocks in a variety of other methods, such as decision trees and matrix factorizations. We suggest an algorithm that gets a finite set of $n$ $d$-dimensional real vectors and returns a weighted subset of $d+1$ vectors whose sum is \emph{exactly} the same. The proof in Caratheodory's Theorem (1907) computes such a subset in $O(n^2d^2)$ time and thus not used in practice. Our algorithm computes this subset in $O(nd)$ time, using $O(\log n)$ calls to Caratheodory's construction on small but "smart" subsets. This is based on a novel paradigm of fusion between different data summarization techniques, known as sketches and coresets. As an example application, we show how it can be used to boost the performance of existing LMS solvers, such as those in scikit-learn library, up to x100. Generalization for streaming and distributed (big) data is trivial. Extensive experimental results and complete open source code are also provided.

Provable Approximations for Constrained $\ell_p$ Regression

The $\ell_p$ linear regression problem is to minimize $f(x)=||Ax-b||_p$ over $x\in\mathbb{R}^d$, where $A\in\mathbb{R}^{n\times d}$, $b\in \mathbb{R}^n$, and $p>0$. To avoid overfitting and bound $||x||_2$, the constrained $\ell_p$ regression minimizes $f(x)$ over every unit vector $x\in\mathbb{R}^d$. This makes the problem non-convex even for the simplest case $d=p=2$. Instead, ridge regression is used to minimize the Lagrange form $f(x)+\lambda ||x||_2$ over $x\in\mathbb{R}^d$, which yields a convex problem in the price of calibrating the regularization parameter $\lambda>0$. We provide the first provable constant factor approximation algorithm that solves the constrained $\ell_p$ regression directly, for every constant $p,d\geq 1$. Using core-sets, its running time is $O(n \log n)$ including extensions for streaming and distributed (big) data. In polynomial time, it can handle outliers, $p\in (0,1)$ and minimize $f(x)$ over every $x$ and permutation of rows in $A$. Experimental results are also provided, including open source and comparison to existing software.