Introduction to Coresets: Approximated Mean
Paper and Code
Nov 04, 2021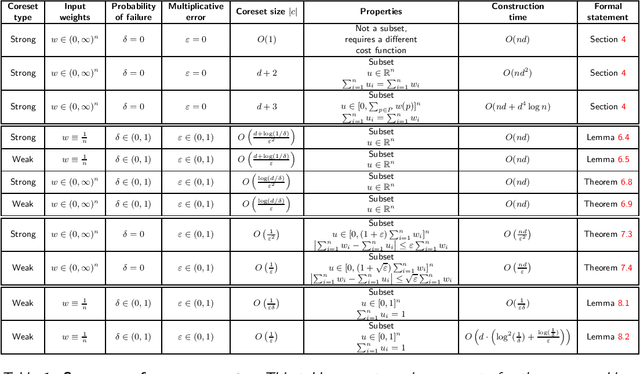
A \emph{strong coreset} for the mean queries of a set $P$ in ${\mathbb{R}}^d$ is a small weighted subset $C\subseteq P$, which provably approximates its sum of squared distances to any center (point) $x\in {\mathbb{R}}^d$. A \emph{weak coreset} is (also) a small weighted subset $C$ of $P$, whose mean approximates the mean of $P$. While computing the mean of $P$ can be easily computed in linear time, its coreset can be used to solve harder constrained version, and is in the heart of generalizations such as coresets for $k$-means clustering. In this paper, we survey most of the mean coreset construction techniques, and suggest a unified analysis methodology for providing and explaining classical and modern results including step-by-step proofs. In particular, we collected folklore and scattered related results, some of which are not formally stated elsewhere. Throughout this survey, we present, explain, and prove a set of techniques, reductions, and algorithms very widespread and crucial in this field. However, when put to use in the (relatively simple) mean problem, such techniques are much simpler to grasp. The survey may help guide new researchers unfamiliar with the field, and introduce them to the very basic foundations of coresets, through a simple, yet fundamental, problem. Experts in this area might appreciate the unified analysis flow, and the comparison table for existing results. Finally, to encourage and help practitioners and software engineers, we provide full open source code for all presented algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge