Training Dynamics of Transformers to Recognize Word Co-occurrence via Gradient Flow Analysis

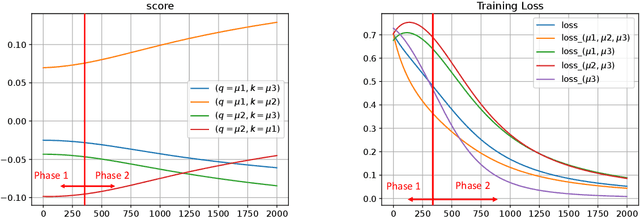
Understanding the training dynamics of transformers is important to explain the impressive capabilities behind large language models. In this work, we study the dynamics of training a shallow transformer on a task of recognizing co-occurrence of two designated words. In the literature of studying training dynamics of transformers, several simplifications are commonly adopted such as weight reparameterization, attention linearization, special initialization, and lazy regime. In contrast, we analyze the gradient flow dynamics of simultaneously training three attention matrices and a linear MLP layer from random initialization, and provide a framework of analyzing such dynamics via a coupled dynamical system. We establish near minimum loss and characterize the attention model after training. We discover that gradient flow serves as an inherent mechanism that naturally divide the training process into two phases. In Phase 1, the linear MLP quickly aligns with the two target signals for correct classification, whereas the softmax attention remains almost unchanged. In Phase 2, the attention matrices and the MLP evolve jointly to enlarge the classification margin and reduce the loss to a near minimum value. Technically, we prove a novel property of the gradient flow, termed \textit{automatic balancing of gradients}, which enables the loss values of different samples to decrease almost at the same rate and further facilitates the proof of near minimum training loss. We also conduct experiments to verify our theoretical results.

Theoretical Characterization of How Neural Network Pruning Affects its Generalization

It has been observed in practice that applying pruning-at-initialization methods to neural networks and training the sparsified networks can not only retain the testing performance of the original dense models, but also sometimes even slightly boost the generalization performance. Theoretical understanding for such experimental observations are yet to be developed. This work makes the first attempt to study how different pruning fractions affect the model's gradient descent dynamics and generalization. Specifically, this work considers a classification task for overparameterized two-layer neural networks, where the network is randomly pruned according to different rates at the initialization. It is shown that as long as the pruning fraction is below a certain threshold, gradient descent can drive the training loss toward zero and the network exhibits good generalization performance. More surprisingly, the generalization bound gets better as the pruning fraction gets larger. To complement this positive result, this work further shows a negative result: there exists a large pruning fraction such that while gradient descent is still able to drive the training loss toward zero (by memorizing noise), the generalization performance is no better than random guessing. This further suggests that pruning can change the feature learning process, which leads to the performance drop of the pruned neural network.

Sharper analysis of sparsely activated wide neural networks with trainable biases

This work studies training one-hidden-layer overparameterized ReLU networks via gradient descent in the neural tangent kernel (NTK) regime, where, differently from the previous works, the networks' biases are trainable and are initialized to some constant rather than zero. The first set of results of this work characterize the convergence of the network's gradient descent dynamics. Surprisingly, it is shown that the network after sparsification can achieve as fast convergence as the original network. The contribution over previous work is that not only the bias is allowed to be updated by gradient descent under our setting but also a finer analysis is given such that the required width to ensure the network's closeness to its NTK is improved. Secondly, the networks' generalization bound after training is provided. A width-sparsity dependence is presented which yields sparsity-dependent localized Rademacher complexity and a generalization bound matching previous analysis (up to logarithmic factors). As a by-product, if the bias initialization is chosen to be zero, the width requirement improves the previous bound for the shallow networks' generalization. Lastly, since the generalization bound has dependence on the smallest eigenvalue of the limiting NTK and the bounds from previous works yield vacuous generalization, this work further studies the least eigenvalue of the limiting NTK. Surprisingly, while it is not shown that trainable biases are necessary, trainable bias helps to identify a nice data-dependent region where a much finer analysis of the NTK's smallest eigenvalue can be conducted, which leads to a much sharper lower bound than the previously known worst-case bound and, consequently, a non-vacuous generalization bound.

On the Neural Tangent Kernel Analysis of Randomly Pruned Wide Neural Networks

We study the behavior of ultra-wide neural networks when their weights are randomly pruned at the initialization, through the lens of neural tangent kernels (NTKs). We show that for fully-connected neural networks when the network is pruned randomly at the initialization, as the width of each layer grows to infinity, the empirical NTK of the pruned neural network converges to that of the original (unpruned) network with some extra scaling factor. Further, if we apply some appropriate scaling after pruning at the initialization, the empirical NTK of the pruned network converges to the exact NTK of the original network, and we provide a non-asymptotic bound on the approximation error in terms of pruning probability. Moreover, when we apply our result to an unpruned network (i.e., we set the probability of pruning a given weight to be zero), our analysis is optimal up to a logarithmic factor in width compared with the result in \cite{arora2019exact}. We conduct experiments to validate our theoretical results. We further test our theory by evaluating random pruning across different architectures via image classification on MNIST and CIFAR-10 and compare its performance with other pruning strategies.