Training Dynamics of Transformers to Recognize Word Co-occurrence via Gradient Flow Analysis
Paper and Code
Oct 12, 2024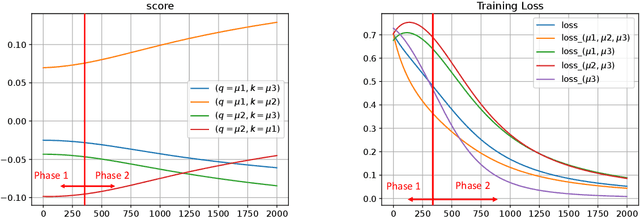
Understanding the training dynamics of transformers is important to explain the impressive capabilities behind large language models. In this work, we study the dynamics of training a shallow transformer on a task of recognizing co-occurrence of two designated words. In the literature of studying training dynamics of transformers, several simplifications are commonly adopted such as weight reparameterization, attention linearization, special initialization, and lazy regime. In contrast, we analyze the gradient flow dynamics of simultaneously training three attention matrices and a linear MLP layer from random initialization, and provide a framework of analyzing such dynamics via a coupled dynamical system. We establish near minimum loss and characterize the attention model after training. We discover that gradient flow serves as an inherent mechanism that naturally divide the training process into two phases. In Phase 1, the linear MLP quickly aligns with the two target signals for correct classification, whereas the softmax attention remains almost unchanged. In Phase 2, the attention matrices and the MLP evolve jointly to enlarge the classification margin and reduce the loss to a near minimum value. Technically, we prove a novel property of the gradient flow, termed \textit{automatic balancing of gradients}, which enables the loss values of different samples to decrease almost at the same rate and further facilitates the proof of near minimum training loss. We also conduct experiments to verify our theoretical results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge