RoLoMa: Robust Loco-Manipulation for Quadruped Robots with Arms

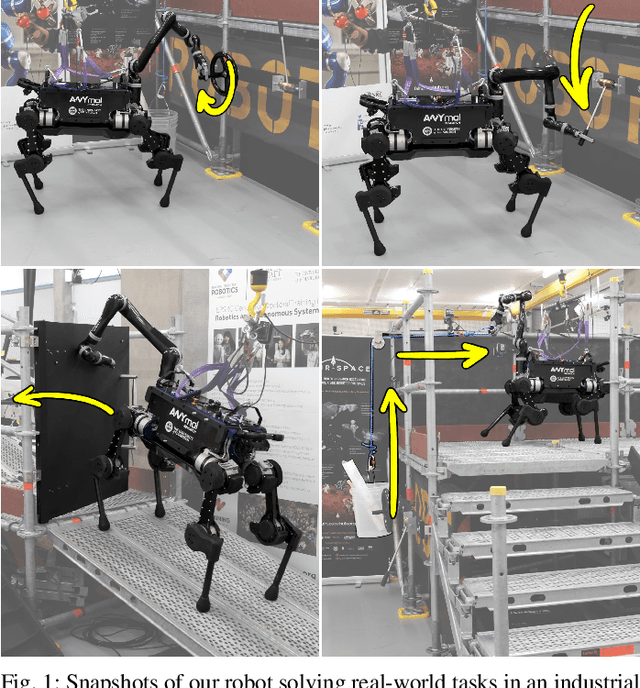
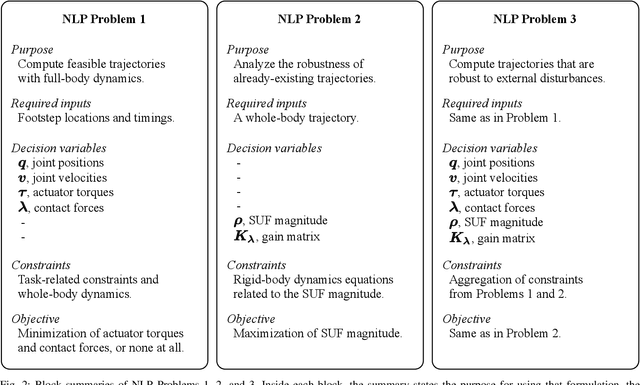
Deployment of robotic systems in the real world requires a certain level of robustness in order to deal with uncertainty factors, such as mismatches in the dynamics model, noise in sensor readings, and communication delays. Some approaches tackle these issues reactively at the control stage. However, regardless of the controller, online motion execution can only be as robust as the system capabilities allow at any given state. This is why it is important to have good motion plans to begin with, where robustness is considered proactively. To this end, we propose a metric (derived from first principles) for representing robustness against external disturbances. We then use this metric within our trajectory optimization framework for solving complex loco-manipulation tasks. Through our experiments, we show that trajectories generated using our approach can resist a greater range of forces originating from any possible direction. By using our method, we can compute trajectories that solve tasks as effectively as before, with the added benefit of being able to counteract stronger disturbances in worst-case scenarios.

Inverse Dynamics vs. Forward Dynamics in Direct Transcription Formulations for Trajectory Optimization

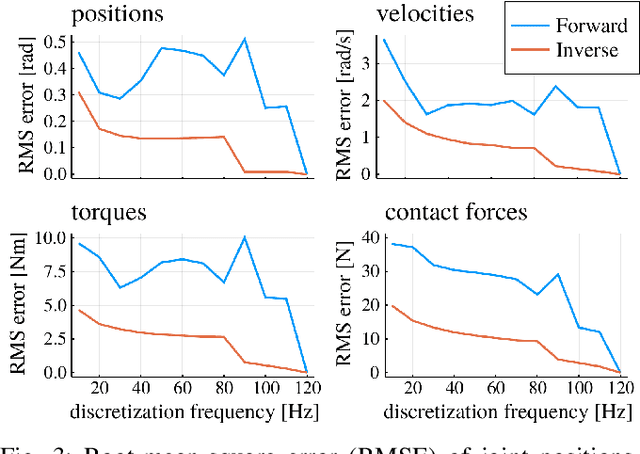
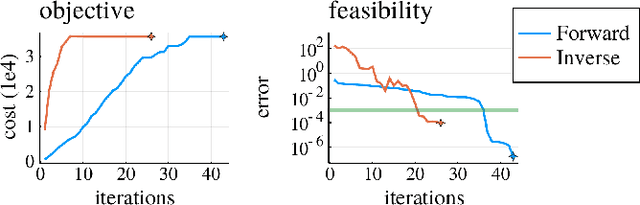
Benchmarks of state-of-the-art rigid-body dynamics libraries have reported better performance for solving the inverse dynamics problem than the forward alternative. Those benchmarks encouraged us to question whether this computational advantage translates to direct transcription formulations, where calculating the rigid-body dynamics and their derivatives often accounts for a significant share of computation time. In this work, we implement an optimization framework where both approaches for enforcing the system dynamics are available. We evaluate the performance of each approach for systems of varying complexity, and for domains with rigid contacts. Our tests revealed that formulations employing inverse dynamics converge faster, require less iterations, and are more robust to coarse problem discretization. These results suggest that inverse dynamics should be the preferred approach to enforce nonlinear system dynamics in simultaneous methods, such as direct transcription.

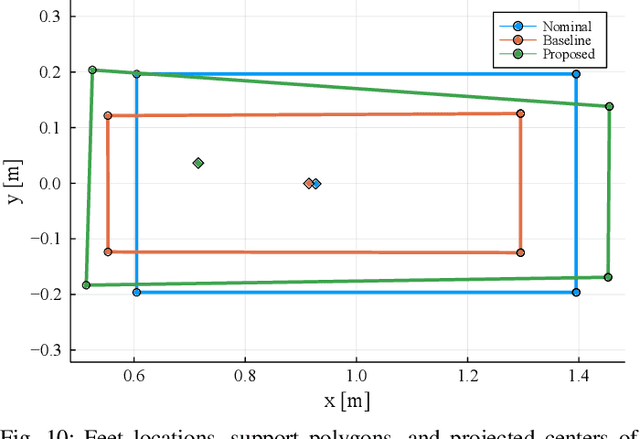
Optimizing Dynamic Trajectories for Robustness to Disturbances Using Polytopic Projections

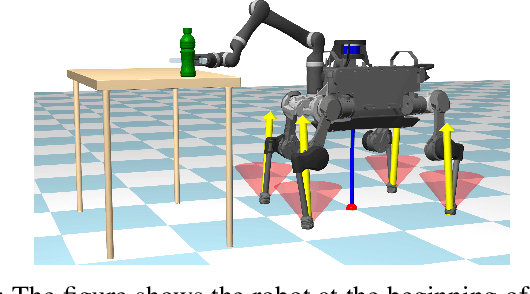
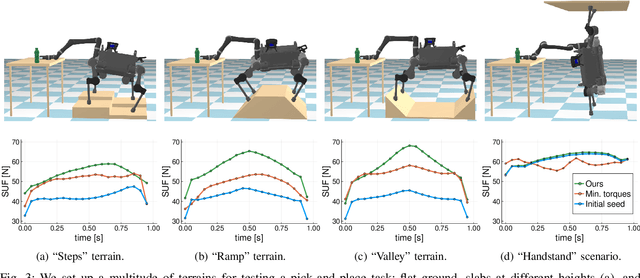
This paper focuses on robustness to disturbance forces and uncertain payloads. We present a novel formulation to optimize the robustness of dynamic trajectories. A straightforward transcription of this formulation into a nonlinear programming problem is not tractable for state-of-the-art solvers, but it is possible to overcome this complication by exploiting the structure induced by the kinematics of the robot. The non-trivial transcription proposed allows trajectory optimization frameworks to converge to highly robust dynamic solutions. We demonstrate the results of our approach using a quadruped robot equipped with a manipulator.

Comparing Metrics for Robustness Against External Perturbations in Dynamic Trajectory Optimization

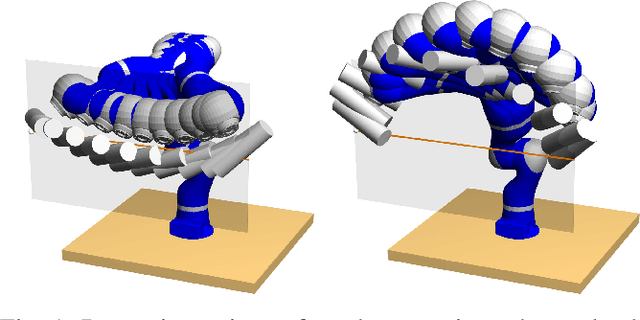
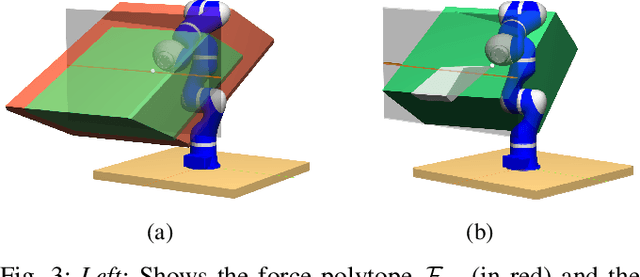
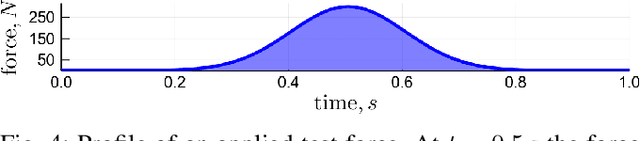
Dynamic trajectory optimization is a popular approach for generating optimal and dynamically consistent trajectories. In order to deal with model errors and perturbations, the trajectories are usually tracked with feedback controllers. Their robustness thus largely depends on the margins of stability and control authority the system retains. Manipulability ellipsoids and force polytopes are well-known tools for evaluating force and motion capabilities of robot manipulators. Increased control authority can be achieved by incorporating task constraints within those tools. However, they come with an increased computational cost. Additionally, their impact on resulting trajectory quality and control authority has not yet been benchmarked and compared. In this letter, we introduce a novel robustness metric, the residual force polytope, which takes the nominal torque required to maintain a posture into account. We further detail a benchmarking protocol including evaluation criteria and visualization tools to compare robustness metrics in dynamic trajectory optimization. To foster benchmarking and allow for reproducibility, we open source a flexible framework for dynamic trajectory optimization via direct transcription along with our benchmark protocols as supplementary materials. Finally, we include - to the best of our knowledge - the first holistic comparison between traditional energy minimization metrics, kinematic manipulability maximization, and force polytope methods.