Inverse Dynamics vs. Forward Dynamics in Direct Transcription Formulations for Trajectory Optimization

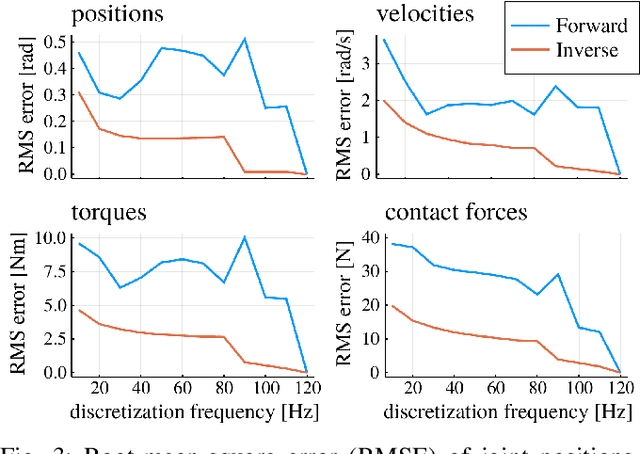
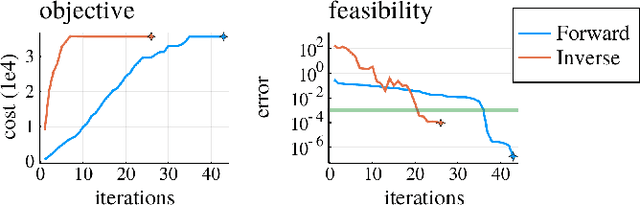
Benchmarks of state-of-the-art rigid-body dynamics libraries have reported better performance for solving the inverse dynamics problem than the forward alternative. Those benchmarks encouraged us to question whether this computational advantage translates to direct transcription formulations, where calculating the rigid-body dynamics and their derivatives often accounts for a significant share of computation time. In this work, we implement an optimization framework where both approaches for enforcing the system dynamics are available. We evaluate the performance of each approach for systems of varying complexity, and for domains with rigid contacts. Our tests revealed that formulations employing inverse dynamics converge faster, require less iterations, and are more robust to coarse problem discretization. These results suggest that inverse dynamics should be the preferred approach to enforce nonlinear system dynamics in simultaneous methods, such as direct transcription.