Optimizing Dynamic Trajectories for Robustness to Disturbances Using Polytopic Projections
Paper and Code
Mar 01, 2020
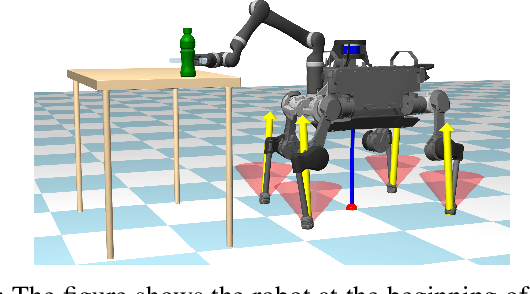
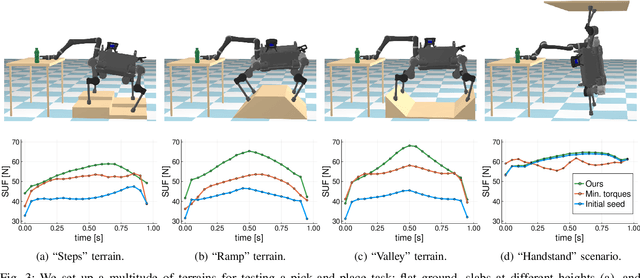

This paper focuses on robustness to disturbance forces and uncertain payloads. We present a novel formulation to optimize the robustness of dynamic trajectories. A straightforward transcription of this formulation into a nonlinear programming problem is not tractable for state-of-the-art solvers, but it is possible to overcome this complication by exploiting the structure induced by the kinematics of the robot. The non-trivial transcription proposed allows trajectory optimization frameworks to converge to highly robust dynamic solutions. We demonstrate the results of our approach using a quadruped robot equipped with a manipulator.
* Under review for IROS 2020
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge