Stochastic Forward-Forward Learning through Representational Dimensionality Compression

The Forward-Forward (FF) algorithm provides a bottom-up alternative to backpropagation (BP) for training neural networks, relying on a layer-wise "goodness" function to guide learning. Existing goodness functions, inspired by energy-based learning (EBL), are typically defined as the sum of squared post-synaptic activations, neglecting the correlations between neurons. In this work, we propose a novel goodness function termed dimensionality compression that uses the effective dimensionality (ED) of fluctuating neural responses to incorporate second-order statistical structure. Our objective minimizes ED for clamped inputs when noise is considered while maximizing it across the sample distribution, promoting structured representations without the need to prepare negative samples. We demonstrate that this formulation achieves competitive performance compared to other non-BP methods. Moreover, we show that noise plays a constructive role that can enhance generalization and improve inference when predictions are derived from the mean of squared outputs, which is equivalent to making predictions based on the energy term. Our findings contribute to the development of more biologically plausible learning algorithms and suggest a natural fit for neuromorphic computing, where stochasticity is a computational resource rather than a nuisance. The code is available at https://github.com/ZhichaoZhu/StochasticForwardForward

Uncertainty Quantification in Working Memory via Moment Neural Networks

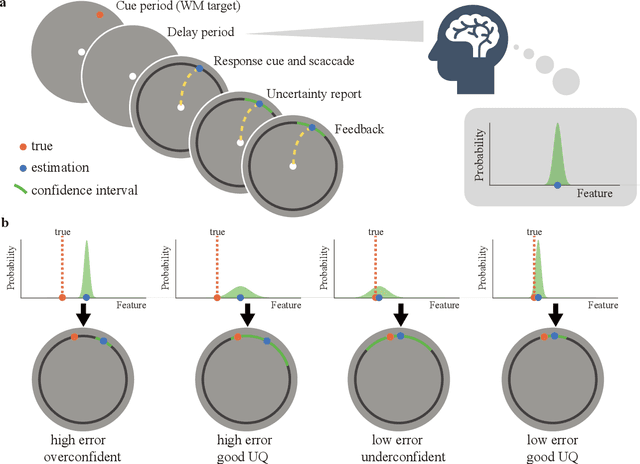
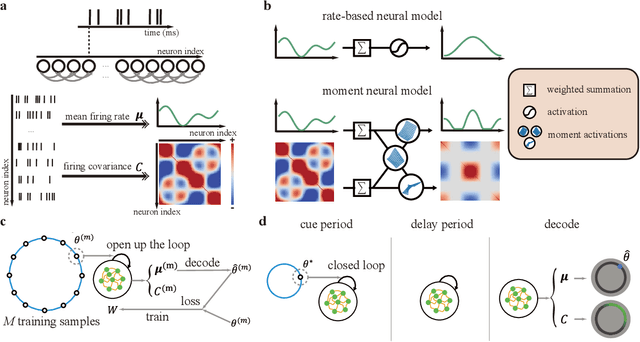
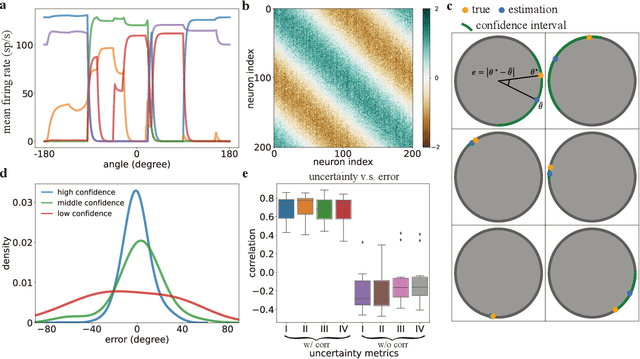
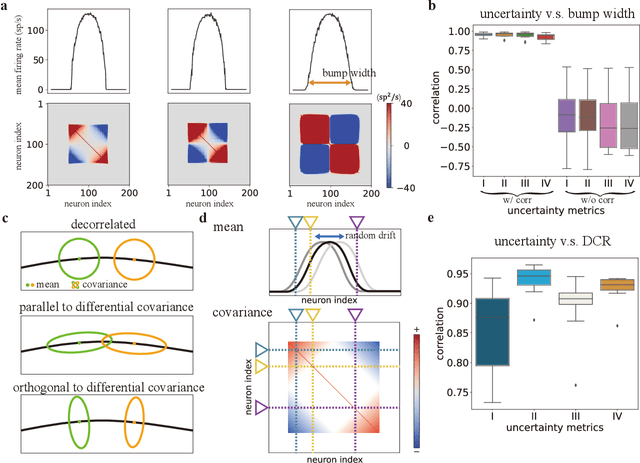
Humans possess a finely tuned sense of uncertainty that helps anticipate potential errors, vital for adaptive behavior and survival. However, the underlying neural mechanisms remain unclear. This study applies moment neural networks (MNNs) to explore the neural mechanism of uncertainty quantification in working memory (WM). The MNN captures nonlinear coupling of the first two moments in spiking neural networks (SNNs), identifying firing covariance as a key indicator of uncertainty in encoded information. Trained on a WM task, the model demonstrates coding precision and uncertainty quantification comparable to human performance. Analysis reveals a link between the probabilistic and sampling-based coding for uncertainty representation. Transferring the MNN's weights to an SNN replicates these results. Furthermore, the study provides testable predictions demonstrating how noise and heterogeneity enhance WM performance, highlighting their beneficial role rather than being mere biological byproducts. These findings offer insights into how the brain effectively manages uncertainty with exceptional accuracy.

Efficient Combinatorial Optimization via Heat Diffusion

Combinatorial optimization problems are widespread but inherently challenging due to their discrete nature.The primary limitation of existing methods is that they can only access a small fraction of the solution space at each iteration, resulting in limited efficiency for searching the global optimal. To overcome this challenge, diverging from conventional efforts of expanding the solver's search scope, we focus on enabling information to actively propagate to the solver through heat diffusion. By transforming the target function while preserving its optima, heat diffusion facilitates information flow from distant regions to the solver, providing more efficient navigation. Utilizing heat diffusion, we propose a framework for solving general combinatorial optimization problems. The proposed methodology demonstrates superior performance across a range of the most challenging and widely encountered combinatorial optimizations. Echoing recent advancements in harnessing thermodynamics for generative artificial intelligence, our study further reveals its significant potential in advancing combinatorial optimization.

Probabilistic Computation with Emerging Covariance: Towards Efficient Uncertainty Quantification

Building robust, interpretable, and secure artificial intelligence system requires some degree of quantifying and representing uncertainty via a probabilistic perspective, as it allows to mimic human cognitive abilities. However, probabilistic computation presents significant challenges due to its inherent complexity. In this paper, we develop an efficient and interpretable probabilistic computation framework by truncating the probabilistic representation up to its first two moments, i.e., mean and covariance. We instantiate the framework by training a deterministic surrogate of a stochastic network that learns the complex probabilistic representation via combinations of simple activations, encapsulating the non-linearities coupling of the mean and covariance. We show that when the mean is supervised for optimizing the task objective, the unsupervised covariance spontaneously emerging from the non-linear coupling with the mean faithfully captures the uncertainty associated with model predictions. Our research highlights the inherent computability and simplicity of probabilistic computation, enabling its wider application in large-scale settings.

Preconditioned Score-based Generative Models

Score-based generative models (SGMs) have recently emerged as a promising class of generative models. However, a fundamental limitation is that their sampling process is slow due to a need for many (\eg, $2000$) iterations of sequential computations. An intuitive acceleration method is to reduce the sampling iterations which however causes severe performance degradation. We assault this problem to the ill-conditioned issues of the Langevin dynamics and reverse diffusion in the sampling process. Under this insight, we propose a model-agnostic {\bf\em preconditioned diffusion sampling} (PDS) method that leverages matrix preconditioning to alleviate the aforementioned problem. PDS alters the sampling process of a vanilla SGM at marginal extra computation cost, and without model retraining. Theoretically, we prove that PDS preserves the output distribution of the SGM, no risk of inducing systematical bias to the original sampling process. We further theoretically reveal a relation between the parameter of PDS and the sampling iterations,easing the parameter estimation under varying sampling iterations. Extensive experiments on various image datasets with a variety of resolutions and diversity validate that our PDS consistently accelerates off-the-shelf SGMs whilst maintaining the synthesis quality. In particular, PDS can accelerate by up to $29\times$ on more challenging high resolution (1024$\times$1024) image generation. Compared with the latest generative models (\eg, CLD-SGM, DDIM, and Analytic-DDIM), PDS can achieve the best sampling quality on CIFAR-10 at a FID score of 1.99. Our code is made publicly available to foster any further research https://github.com/fudan-zvg/PDS.

Accelerating Score-based Generative Models with Preconditioned Diffusion Sampling

Score-based generative models (SGMs) have recently emerged as a promising class of generative models. However, a fundamental limitation is that their inference is very slow due to a need for many (e.g., 2000) iterations of sequential computations. An intuitive acceleration method is to reduce the sampling iterations which however causes severe performance degradation. We investigate this problem by viewing the diffusion sampling process as a Metropolis adjusted Langevin algorithm, which helps reveal the underlying cause to be ill-conditioned curvature. Under this insight, we propose a model-agnostic preconditioned diffusion sampling (PDS) method that leverages matrix preconditioning to alleviate the aforementioned problem. Crucially, PDS is proven theoretically to converge to the original target distribution of a SGM, no need for retraining. Extensive experiments on three image datasets with a variety of resolutions and diversity validate that PDS consistently accelerates off-the-shelf SGMs whilst maintaining the synthesis quality. In particular, PDS can accelerate by up to 29x on more challenging high resolution (1024x1024) image generation.

Accelerating Score-based Generative Models for High-Resolution Image Synthesis

Score-based generative models (SGMs) have recently emerged as a promising class of generative models. The key idea is to produce high-quality images by recurrently adding Gaussian noises and gradients to a Gaussian sample until converging to the target distribution, a.k.a. the diffusion sampling. To ensure stability of convergence in sampling and generation quality, however, this sequential sampling process has to take a small step size and many sampling iterations (e.g., 2000). Several acceleration methods have been proposed with focus on low-resolution generation. In this work, we consider the acceleration of high-resolution generation with SGMs, a more challenging yet more important problem. We prove theoretically that this slow convergence drawback is primarily due to the ignorance of the target distribution. Further, we introduce a novel Target Distribution Aware Sampling (TDAS) method by leveraging the structural priors in space and frequency domains. Extensive experiments on CIFAR-10, CelebA, LSUN, and FFHQ datasets validate that TDAS can consistently accelerate state-of-the-art SGMs, particularly on more challenging high resolution (1024x1024) image generation tasks by up to 18.4x, whilst largely maintaining the synthesis quality. With fewer sampling iterations, TDAS can still generate good quality images. In contrast, the existing methods degrade drastically or even fails completely