Advantages of Neural Population Coding for Deep Learning

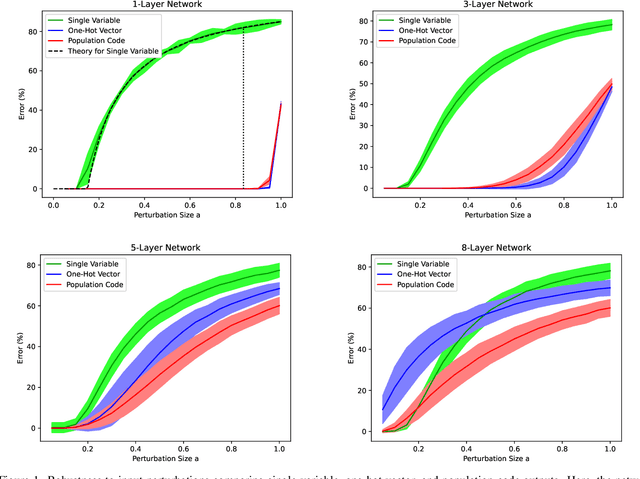
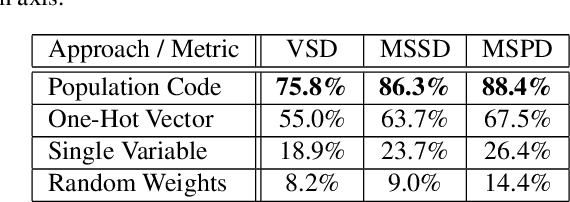
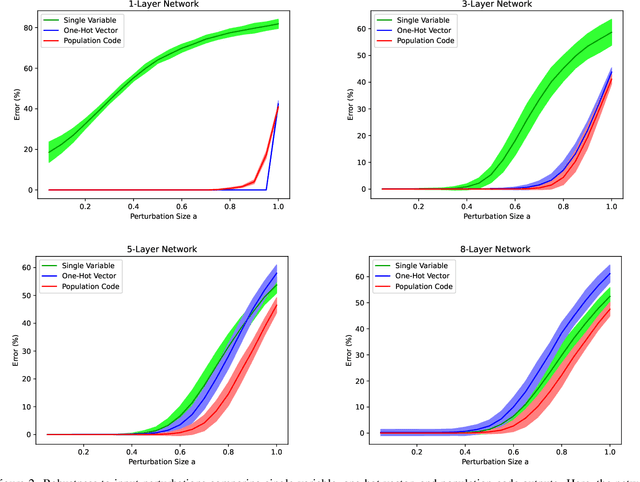
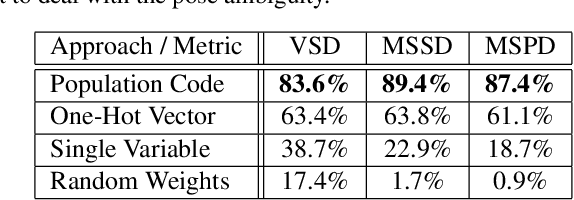
Scalar variables, e.g., the orientation of a shape in an image, are commonly predicted using a single output neuron in a neural network. In contrast, the mammalian cortex represents variables with a population of neurons. In this population code, each neuron is most active at its preferred value and shows partial activity for other values. Here, we investigate the benefit of using a population code for the output layer of a neural network. We compare population codes against single-neuron outputs and one-hot vectors. First, we show theoretically and in experiments with synthetic data that population codes improve robustness to input noise in networks of stacked linear layers. Second, we demonstrate the benefit of using population codes to encode ambiguous outputs, such as the pose of symmetric objects. Using the T-LESS dataset of feature-less real-world objects, we show that population codes improve the accuracy of predicting 3D object orientation from image input.

Few-Shot Image Classification Along Sparse Graphs

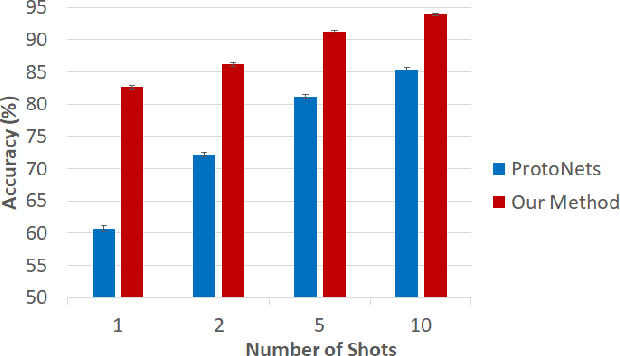
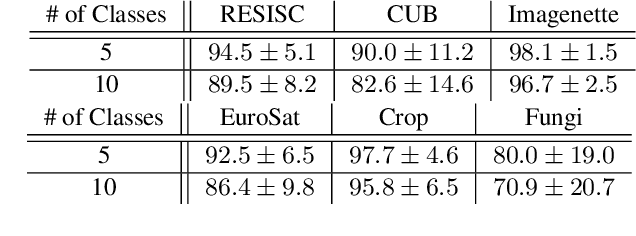
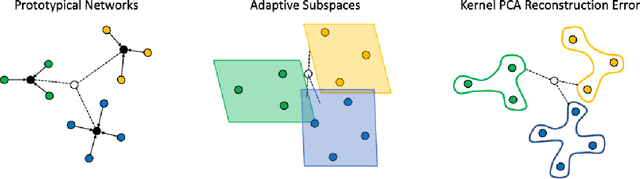
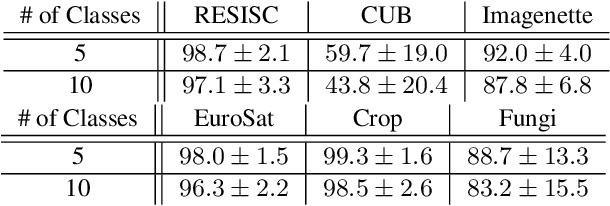
Few-shot learning remains a challenging problem, with unsatisfactory 1-shot accuracies for most real-world data. Here, we present a different perspective for data distributions in the feature space of a deep network and show how to exploit it for few-shot learning. First, we observe that nearest neighbors in the feature space are with high probability members of the same class while generally two random points from one class are not much closer to each other than points from different classes. This observation suggests that classes in feature space form sparse, loosely connected graphs instead of dense clusters. To exploit this property, we propose using a small amount of label propagation into the unlabeled space and then using a kernel PCA reconstruction error as decision boundary for the feature-space data distribution of each class. Using this method, which we call "K-Prop," we demonstrate largely improved few-shot learning performances (e.g., 83% accuracy for 1-shot 5-way classification on the RESISC45 satellite-images dataset) for datasets for which a backbone network can be trained with high within-class nearest-neighbor probabilities. We demonstrate this relationship using six different datasets.

Set Representation Learning with Generalized Sliced-Wasserstein Embeddings

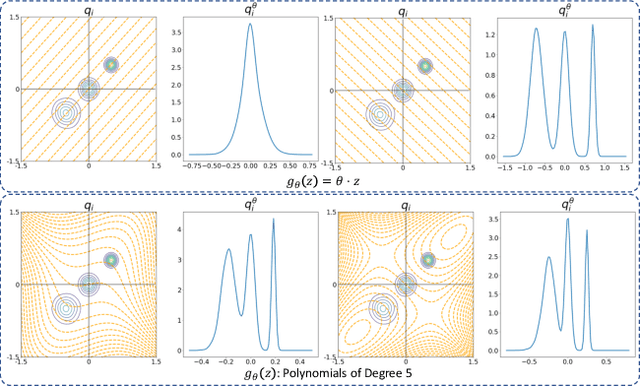
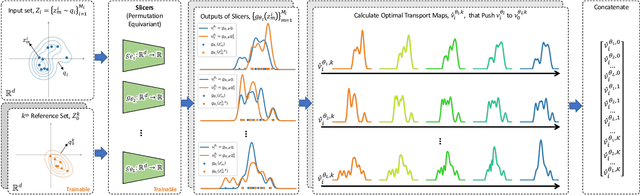
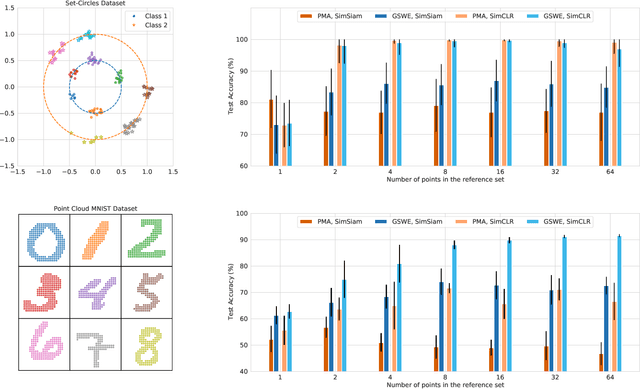
An increasing number of machine learning tasks deal with learning representations from set-structured data. Solutions to these problems involve the composition of permutation-equivariant modules (e.g., self-attention, or individual processing via feed-forward neural networks) and permutation-invariant modules (e.g., global average pooling, or pooling by multi-head attention). In this paper, we propose a geometrically-interpretable framework for learning representations from set-structured data, which is rooted in the optimal mass transportation problem. In particular, we treat elements of a set as samples from a probability measure and propose an exact Euclidean embedding for Generalized Sliced Wasserstein (GSW) distances to learn from set-structured data effectively. We evaluate our proposed framework on multiple supervised and unsupervised set learning tasks and demonstrate its superiority over state-of-the-art set representation learning approaches.

Wasserstein Embedding for Graph Learning

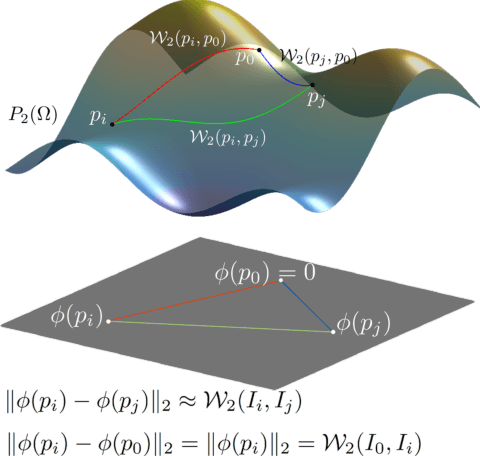
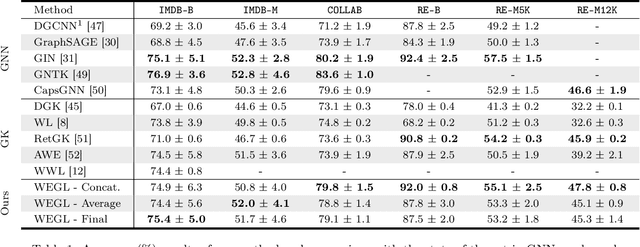
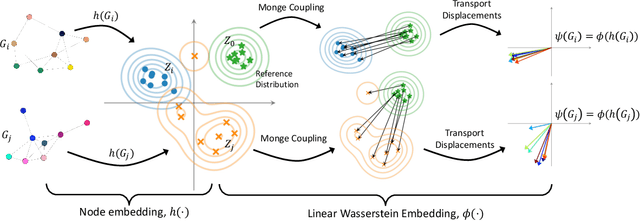
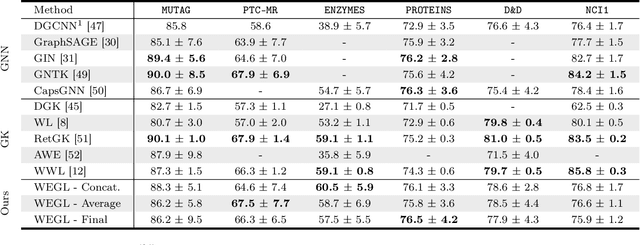
We present Wasserstein Embedding for Graph Learning (WEGL), a novel and fast framework for embedding entire graphs in a vector space, in which various machine learning models are applicable for graph-level prediction tasks. We leverage new insights on defining similarity between graphs as a function of the similarity between their node embedding distributions. Specifically, we use the Wasserstein distance to measure the dissimilarity between node embeddings of different graphs. Different from prior work, we avoid pairwise calculation of distances between graphs and reduce the computational complexity from quadratic to linear in the number of graphs. WEGL calculates Monge maps from a reference distribution to each node embedding and, based on these maps, creates a fixed-sized vector representation of the graph. We evaluate our new graph embedding approach on various benchmark graph-property prediction tasks, showing state-of-the-art classification performance, while having superior computational efficiency.

Universal Litmus Patterns: Revealing Backdoor Attacks in CNNs

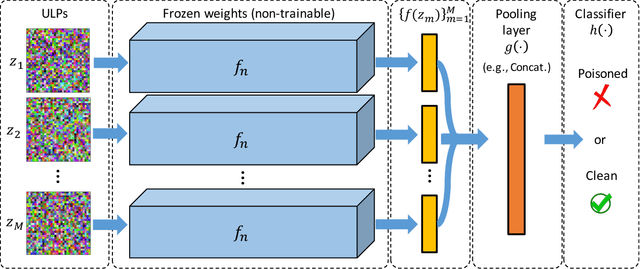
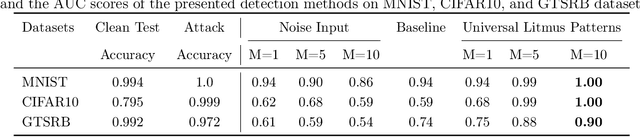
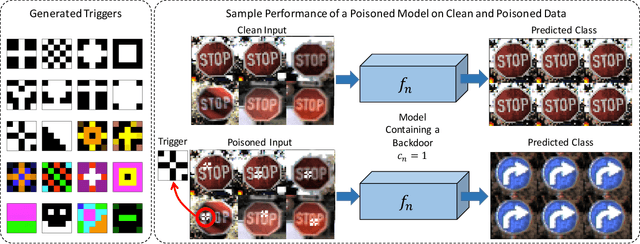
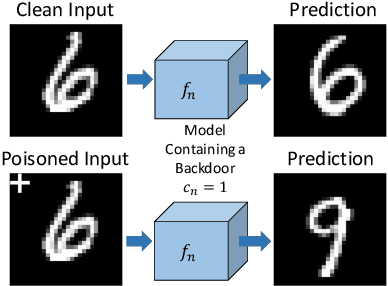
The unprecedented success of deep neural networks in various applications have made these networks a prime target for adversarial exploitation. In this paper, we introduce a benchmark technique for detecting backdoor attacks (aka Trojan attacks) on deep convolutional neural networks (CNNs). We introduce the concept of Universal Litmus Patterns (ULPs), which enable one to reveal backdoor attacks by feeding these universal patterns to the network and analyzing the output (i.e., classifying as `clean' or `corrupted'). This detection is fast because it requires only a few forward passes through a CNN. We demonstrate the effectiveness of ULPs for detecting backdoor attacks on thousands of networks trained on three benchmark datasets, namely the German Traffic Sign Recognition Benchmark (GTSRB), MNIST, and CIFAR10.

Discovering Molecular Functional Groups Using Graph Convolutional Neural Networks

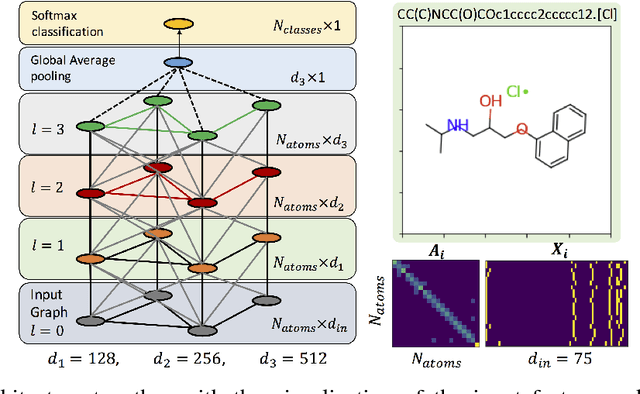
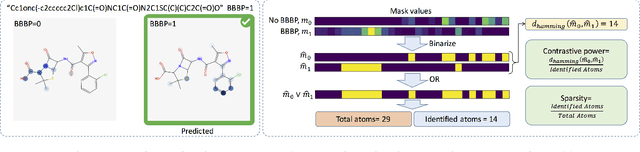
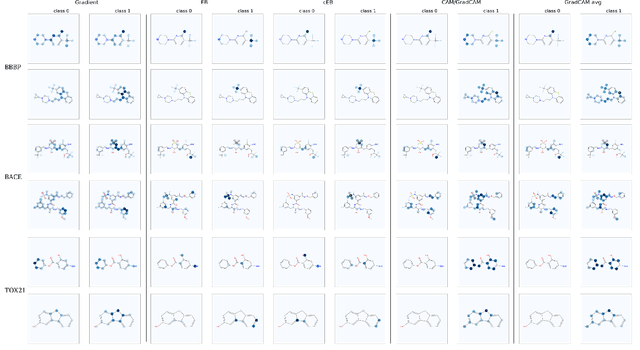
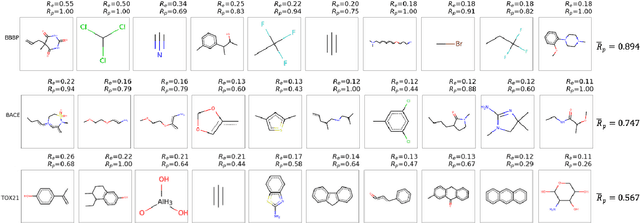
Functional groups (FGs) serve as a foundation for analyzing chemical properties of organic molecules. Automatic discovery of FGs will impact various fields of research, including medicinal chemistry, by reducing the amount of lab experiments required for discovery or synthesis of new molecules. Here, we investigate methods based on graph convolutional neural networks (GCNNs) for localizing FGs that contribute to specific chemical properties. Molecules are modeled as undirected graphs with atoms as nodes and bonds as edges. Using this graph structure, we trained GCNNs in a supervised way on experimentally-validated molecular training sets to predict specific chemical properties, e.g., toxicity. Upon learning a GCNN, we analyzed its activation patterns to automatically identify FGs using four different methods: gradient-based saliency maps, Class Activation Mapping (CAM), gradient-weighted CAM (Grad-CAM), and Excitation Back-Propagation. We evaluated the contrastive power of these methods with respect to the specificity of the identified molecular substructures and their relevance for chemical functions. Grad- CAM had the highest contrastive power and generated qualitatively the best FGs. This work paves the way for automatic analysis and design of new molecules.

Sliced Wasserstein Distance for Learning Gaussian Mixture Models

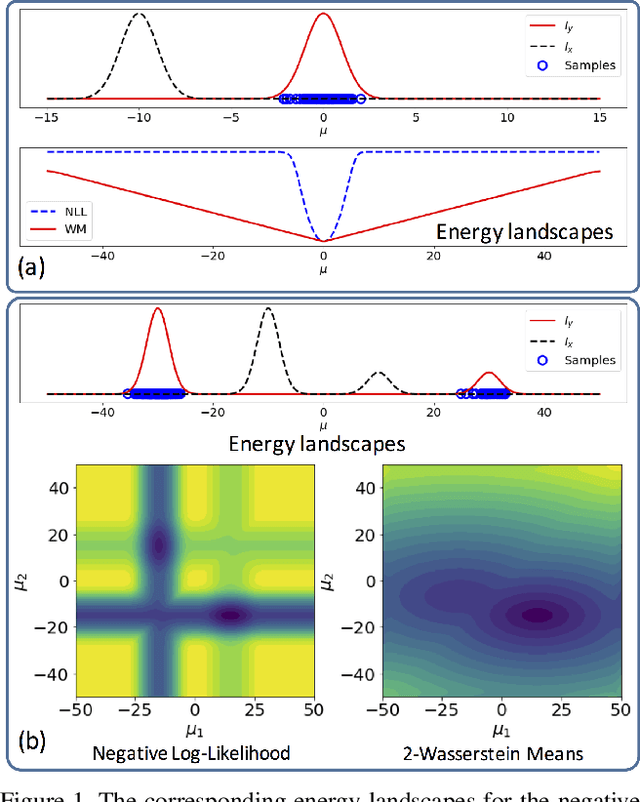
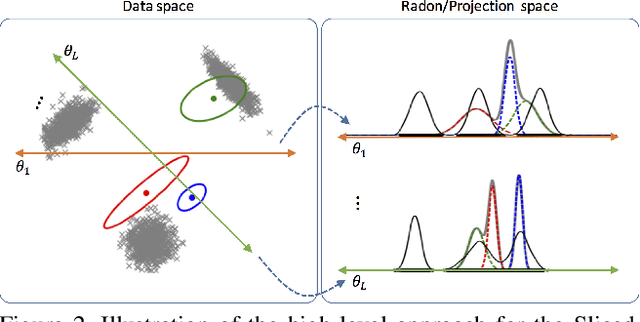
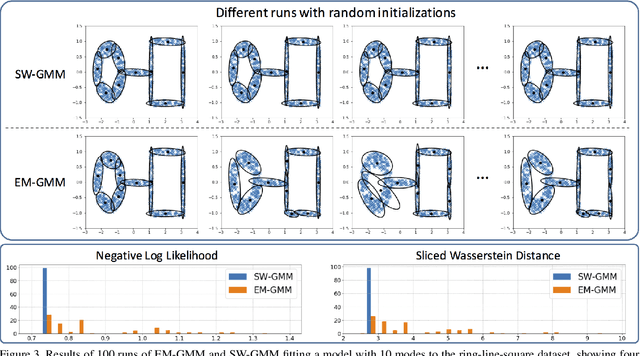
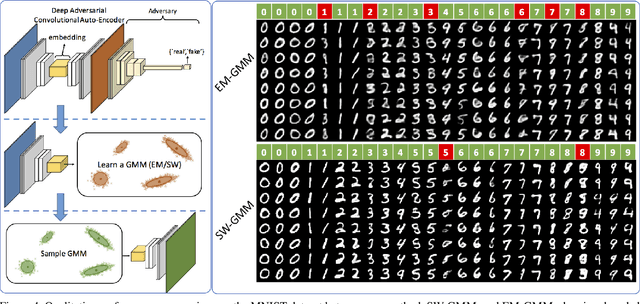
Gaussian mixture models (GMM) are powerful parametric tools with many applications in machine learning and computer vision. Expectation maximization (EM) is the most popular algorithm for estimating the GMM parameters. However, EM guarantees only convergence to a stationary point of the log-likelihood function, which could be arbitrarily worse than the optimal solution. Inspired by the relationship between the negative log-likelihood function and the Kullback-Leibler (KL) divergence, we propose an alternative formulation for estimating the GMM parameters using the sliced Wasserstein distance, which gives rise to a new algorithm. Specifically, we propose minimizing the sliced-Wasserstein distance between the mixture model and the data distribution with respect to the GMM parameters. In contrast to the KL-divergence, the energy landscape for the sliced-Wasserstein distance is more well-behaved and therefore more suitable for a stochastic gradient descent scheme to obtain the optimal GMM parameters. We show that our formulation results in parameter estimates that are more robust to random initializations and demonstrate that it can estimate high-dimensional data distributions more faithfully than the EM algorithm.