Reduced-Set Kernel Principal Components Analysis for Improving the Training and Execution Speed of Kernel Machines

This paper presents a practical, and theoretically well-founded, approach to improve the speed of kernel manifold learning algorithms relying on spectral decomposition. Utilizing recent insights in kernel smoothing and learning with integral operators, we propose Reduced Set KPCA (RSKPCA), which also suggests an easy-to-implement method to remove or replace samples with minimal effect on the empirical operator. A simple data point selection procedure is given to generate a substitute density for the data, with accuracy that is governed by a user-tunable parameter . The effect of the approximation on the quality of the KPCA solution, in terms of spectral and operator errors, can be shown directly in terms of the density estimate error and as a function of the parameter . We show in experiments that RSKPCA can improve both training and evaluation time of KPCA by up to an order of magnitude, and compares favorably to the widely-used Nystrom and density-weighted Nystrom methods.

Linear, Deterministic, and Order-Invariant Initialization Methods for the K-Means Clustering Algorithm

Over the past five decades, k-means has become the clustering algorithm of choice in many application domains primarily due to its simplicity, time/space efficiency, and invariance to the ordering of the data points. Unfortunately, the algorithm's sensitivity to the initial selection of the cluster centers remains to be its most serious drawback. Numerous initialization methods have been proposed to address this drawback. Many of these methods, however, have time complexity superlinear in the number of data points, which makes them impractical for large data sets. On the other hand, linear methods are often random and/or sensitive to the ordering of the data points. These methods are generally unreliable in that the quality of their results is unpredictable. Therefore, it is common practice to perform multiple runs of such methods and take the output of the run that produces the best results. Such a practice, however, greatly increases the computational requirements of the otherwise highly efficient k-means algorithm. In this chapter, we investigate the empirical performance of six linear, deterministic (non-random), and order-invariant k-means initialization methods on a large and diverse collection of data sets from the UCI Machine Learning Repository. The results demonstrate that two relatively unknown hierarchical initialization methods due to Su and Dy outperform the remaining four methods with respect to two objective effectiveness criteria. In addition, a recent method due to Erisoglu et al. performs surprisingly poorly.

Deterministic Initialization of the K-Means Algorithm Using Hierarchical Clustering

K-means is undoubtedly the most widely used partitional clustering algorithm. Unfortunately, due to its gradient descent nature, this algorithm is highly sensitive to the initial placement of the cluster centers. Numerous initialization methods have been proposed to address this problem. Many of these methods, however, have superlinear complexity in the number of data points, making them impractical for large data sets. On the other hand, linear methods are often random and/or order-sensitive, which renders their results unrepeatable. Recently, Su and Dy proposed two highly successful hierarchical initialization methods named Var-Part and PCA-Part that are not only linear, but also deterministic (non-random) and order-invariant. In this paper, we propose a discriminant analysis based approach that addresses a common deficiency of these two methods. Experiments on a large and diverse collection of data sets from the UCI Machine Learning Repository demonstrate that Var-Part and PCA-Part are highly competitive with one of the best random initialization methods to date, i.e., k-means++, and that the proposed approach significantly improves the performance of both hierarchical methods.

A Comparative Study of Efficient Initialization Methods for the K-Means Clustering Algorithm

K-means is undoubtedly the most widely used partitional clustering algorithm. Unfortunately, due to its gradient descent nature, this algorithm is highly sensitive to the initial placement of the cluster centers. Numerous initialization methods have been proposed to address this problem. In this paper, we first present an overview of these methods with an emphasis on their computational efficiency. We then compare eight commonly used linear time complexity initialization methods on a large and diverse collection of data sets using various performance criteria. Finally, we analyze the experimental results using non-parametric statistical tests and provide recommendations for practitioners. We demonstrate that popular initialization methods often perform poorly and that there are in fact strong alternatives to these methods.

Comments on "On Approximating Euclidean Metrics by Weighted t-Cost Distances in Arbitrary Dimension"

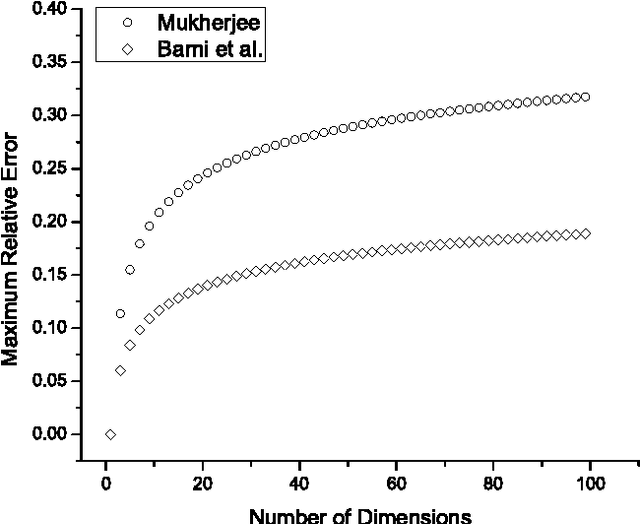
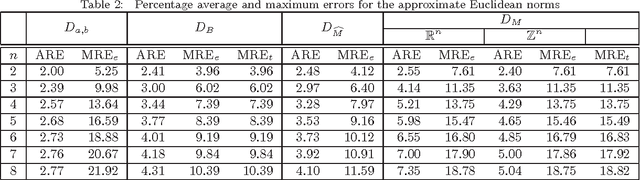
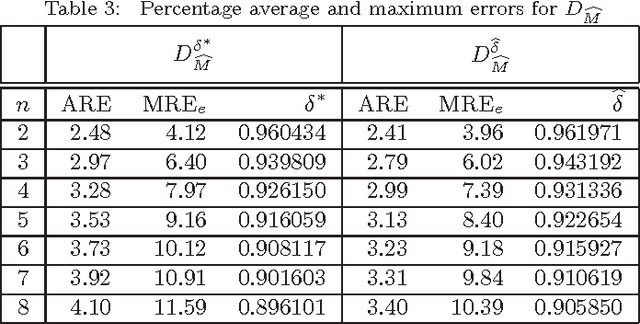
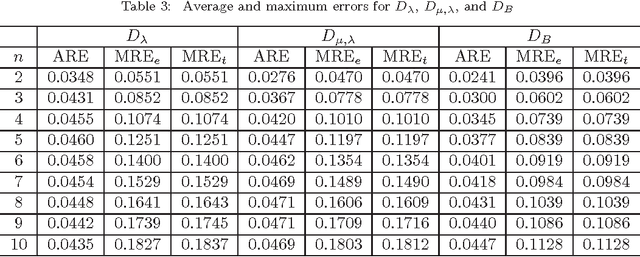
Mukherjee (Pattern Recognition Letters, vol. 32, pp. 824-831, 2011) recently introduced a class of distance functions called weighted t-cost distances that generalize m-neighbor, octagonal, and t-cost distances. He proved that weighted t-cost distances form a family of metrics and derived an approximation for the Euclidean norm in $\mathbb{Z}^n$. In this note we compare this approximation to two previously proposed Euclidean norm approximations and demonstrate that the empirical average errors given by Mukherjee are significantly optimistic in $\mathbb{R}^n$. We also propose a simple normalization scheme that improves the accuracy of his approximation substantially with respect to both average and maximum relative errors.

Nonlinear Vector Filtering for Impulsive Noise Removal from Color Images

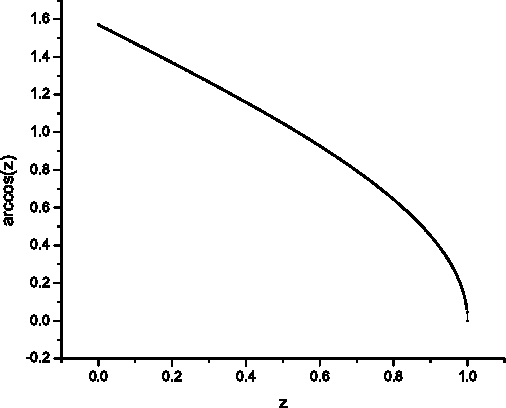
In this paper, a comprehensive survey of 48 filters for impulsive noise removal from color images is presented. The filters are formulated using a uniform notation and categorized into 8 families. The performance of these filters is compared on a large set of images that cover a variety of domains using three effectiveness and one efficiency criteria. In order to ensure a fair efficiency comparison, a fast and accurate approximation for the inverse cosine function is introduced. In addition, commonly used distance measures (Minkowski, angular, and directional-distance) are analyzed and evaluated. Finally, suggestions are provided on how to choose a filter given certain requirements.

A Fast Switching Filter for Impulsive Noise Removal from Color Images

In this paper, we present a fast switching filter for impulsive noise removal from color images. The filter exploits the HSL color space, and is based on the peer group concept, which allows for the fast detection of noise in a neighborhood without resorting to pairwise distance computations between each pixel. Experiments on large set of diverse images demonstrate that the proposed approach is not only extremely fast, but also gives excellent results in comparison to various state-of-the-art filters.

Cost-Effective Implementation of Order-Statistics Based Vector Filters Using Minimax Approximations

Vector operators based on robust order statistics have proved successful in digital multichannel imaging applications, particularly color image filtering and enhancement, in dealing with impulsive noise while preserving edges and fine image details. These operators often have very high computational requirements which limits their use in time-critical applications. This paper introduces techniques to speed up vector filters using the minimax approximation theory. Extensive experiments on a large and diverse set of color images show that proposed approximations achieve an excellent balance among ease of implementation, accuracy, and computational speed.

On Euclidean Norm Approximations

Euclidean norm calculations arise frequently in scientific and engineering applications. Several approximations for this norm with differing complexity and accuracy have been proposed in the literature. Earlier approaches were based on minimizing the maximum error. Recently, Seol and Cheun proposed an approximation based on minimizing the average error. In this paper, we first examine these approximations in detail, show that they fit into a single mathematical formulation, and compare their average and maximum errors. We then show that the maximum errors given by Seol and Cheun are significantly optimistic.