Comments on "On Approximating Euclidean Metrics by Weighted t-Cost Distances in Arbitrary Dimension"
Paper and Code
Jun 10, 2012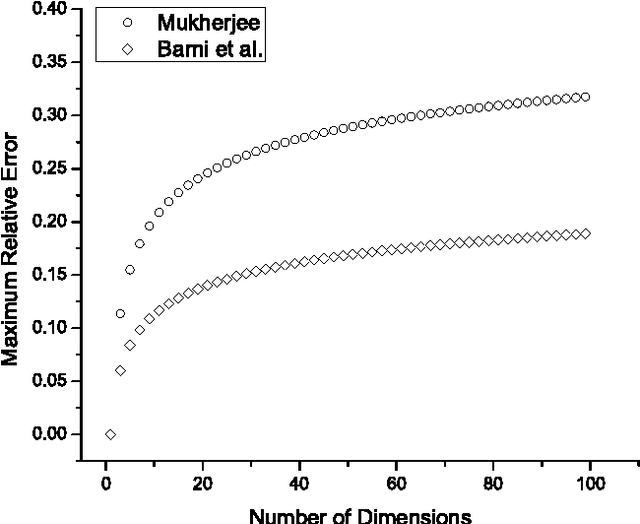

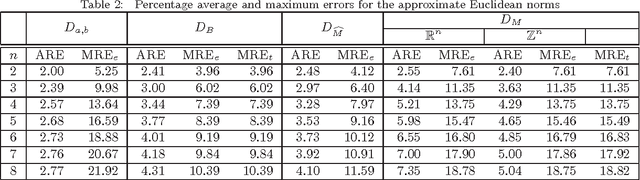
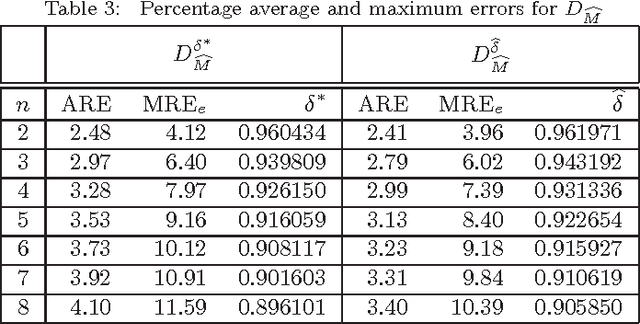
Mukherjee (Pattern Recognition Letters, vol. 32, pp. 824-831, 2011) recently introduced a class of distance functions called weighted t-cost distances that generalize m-neighbor, octagonal, and t-cost distances. He proved that weighted t-cost distances form a family of metrics and derived an approximation for the Euclidean norm in $\mathbb{Z}^n$. In this note we compare this approximation to two previously proposed Euclidean norm approximations and demonstrate that the empirical average errors given by Mukherjee are significantly optimistic in $\mathbb{R}^n$. We also propose a simple normalization scheme that improves the accuracy of his approximation substantially with respect to both average and maximum relative errors.
* Pattern Recognition Letters 33 (2012) 1422--1425 * 7 pages, 1 figure, 3 tables. arXiv admin note: substantial text
overlap with arXiv:1008.4870
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge