Comments on "On Approximating Euclidean Metrics by Weighted t-Cost Distances in Arbitrary Dimension"

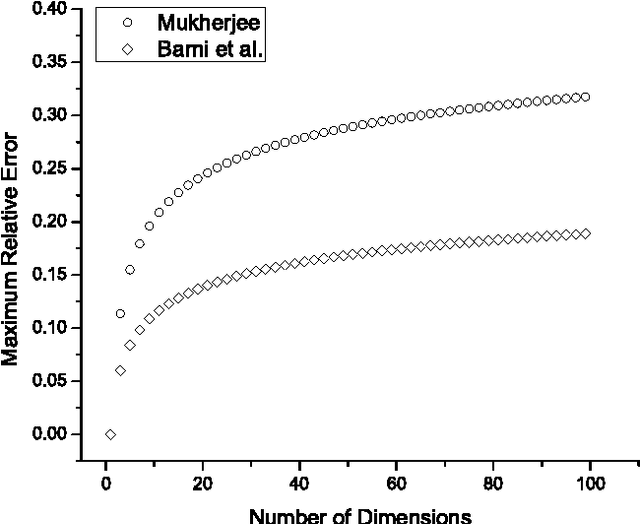
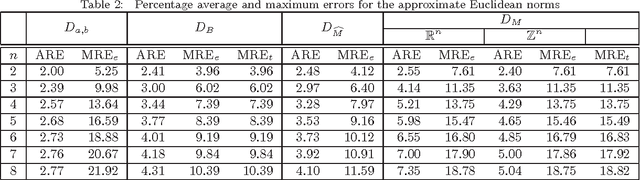
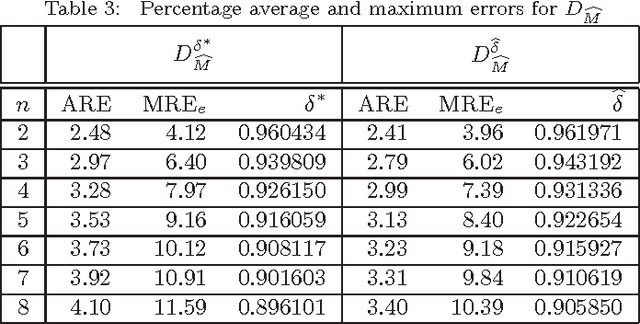
Mukherjee (Pattern Recognition Letters, vol. 32, pp. 824-831, 2011) recently introduced a class of distance functions called weighted t-cost distances that generalize m-neighbor, octagonal, and t-cost distances. He proved that weighted t-cost distances form a family of metrics and derived an approximation for the Euclidean norm in $\mathbb{Z}^n$. In this note we compare this approximation to two previously proposed Euclidean norm approximations and demonstrate that the empirical average errors given by Mukherjee are significantly optimistic in $\mathbb{R}^n$. We also propose a simple normalization scheme that improves the accuracy of his approximation substantially with respect to both average and maximum relative errors.

Cost-Effective Implementation of Order-Statistics Based Vector Filters Using Minimax Approximations

Vector operators based on robust order statistics have proved successful in digital multichannel imaging applications, particularly color image filtering and enhancement, in dealing with impulsive noise while preserving edges and fine image details. These operators often have very high computational requirements which limits their use in time-critical applications. This paper introduces techniques to speed up vector filters using the minimax approximation theory. Extensive experiments on a large and diverse set of color images show that proposed approximations achieve an excellent balance among ease of implementation, accuracy, and computational speed.

Fast Color Space Transformations Using Minimax Approximations

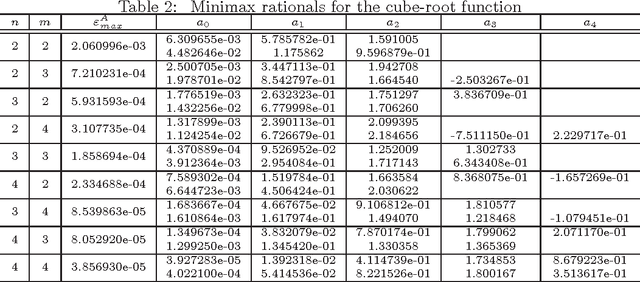
Color space transformations are frequently used in image processing, graphics, and visualization applications. In many cases, these transformations are complex nonlinear functions, which prohibits their use in time-critical applications. In this paper, we present a new approach called Minimax Approximations for Color-space Transformations (MACT).We demonstrate MACT on three commonly used color space transformations. Extensive experiments on a large and diverse image set and comparisons with well-known multidimensional lookup table interpolation methods show that MACT achieves an excellent balance among four criteria: ease of implementation, memory usage, accuracy, and computational speed.

On Euclidean Norm Approximations

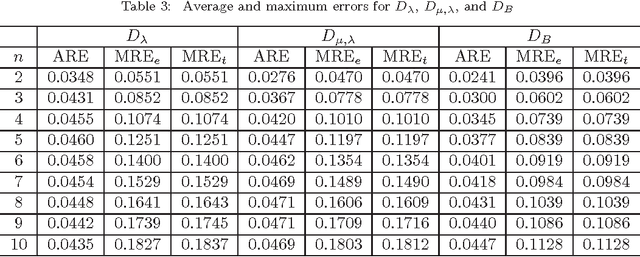
Euclidean norm calculations arise frequently in scientific and engineering applications. Several approximations for this norm with differing complexity and accuracy have been proposed in the literature. Earlier approaches were based on minimizing the maximum error. Recently, Seol and Cheun proposed an approximation based on minimizing the average error. In this paper, we first examine these approximations in detail, show that they fit into a single mathematical formulation, and compare their average and maximum errors. We then show that the maximum errors given by Seol and Cheun are significantly optimistic.