Online Matching: A Real-time Bandit System for Large-scale Recommendations

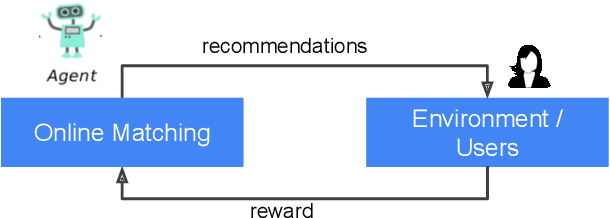
The last decade has witnessed many successes of deep learning-based models for industry-scale recommender systems. These models are typically trained offline in a batch manner. While being effective in capturing users' past interactions with recommendation platforms, batch learning suffers from long model-update latency and is vulnerable to system biases, making it hard to adapt to distribution shift and explore new items or user interests. Although online learning-based approaches (e.g., multi-armed bandits) have demonstrated promising theoretical results in tackling these challenges, their practical real-time implementation in large-scale recommender systems remains limited. First, the scalability of online approaches in servicing a massive online traffic while ensuring timely updates of bandit parameters poses a significant challenge. Additionally, exploring uncertainty in recommender systems can easily result in unfavorable user experience, highlighting the need for devising intricate strategies that effectively balance the trade-off between exploitation and exploration. In this paper, we introduce Online Matching: a scalable closed-loop bandit system learning from users' direct feedback on items in real time. We present a hybrid "offline + online" approach for constructing this system, accompanied by a comprehensive exposition of the end-to-end system architecture. We propose Diag-LinUCB -- a novel extension of the LinUCB algorithm -- to enable distributed updates of bandits parameter in a scalable and timely manner. We conduct live experiments in YouTube and show that Online Matching is able to enhance the capabilities of fresh content discovery and item exploration in the present platform.

Scalable K-Medoids via True Error Bound and Familywise Bandits

K-Medoids(KM) is a standard clustering method, used extensively on semi-metric data. Error analyses of KM have traditionally used an in-sample notion of error, which can be far from the true error and suffer from generalization error. We formalize the true K-Medoid error based on the underlying data distribution, by decomposing it into fundamental statistical problems of: minimum estimation (ME) and minimum mean estimation (MME). We provide a convergence result for MME and bound the true KM error for iid data. Inspired by this bound, we propose a computationally efficient, distributed KM algorithm namely MCPAM. MCPAM has expected runtime $\mathcal{O}(km)$ and provides massive computational savings for a small tradeoff in accuracy. We verify the quality and scaling properties of MCPAM on various datasets. And achieve the hitherto unachieved feat of calculating the KM of 1 billion points on semi-metric spaces.