EFIM: Efficient Serving of LLMs for Infilling Tasks with Improved KV Cache Reuse

Large language models (LLMs) are often used for infilling tasks, which involve predicting or generating missing information in a given text. These tasks typically require multiple interactions with similar context. To reduce the computation of repeated historical tokens, cross-request key-value (KV) cache reuse, a technique that stores and reuses intermediate computations, has become a crucial method in multi-round interactive services. However, in infilling tasks, the KV cache reuse is often hindered by the structure of the prompt format, which typically consists of a prefix and suffix relative to the insertion point. Specifically, the KV cache of the prefix or suffix part is frequently invalidated as the other part (suffix or prefix) is incrementally generated. To address the issue, we propose EFIM, a transformed prompt format of FIM to unleash the performance potential of KV cache reuse. Although the transformed prompt can solve the inefficiency, it exposes subtoken generation problems in current LLMs, where they have difficulty generating partial words accurately. Therefore, we introduce a fragment tokenization training method which splits text into multiple fragments before tokenization during data processing. Experiments on two representative LLMs show that LLM serving with EFIM can lower the latency by 52% and improve the throughput by 98% while maintaining the original infilling capability. EFIM's source code is publicly available at https://github.com/gty111/EFIM.

AutoDebias: Learning to Debias for Recommendation

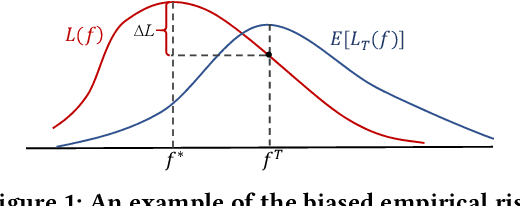
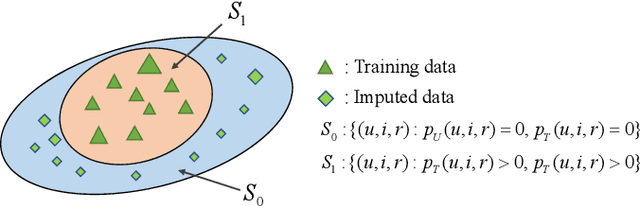
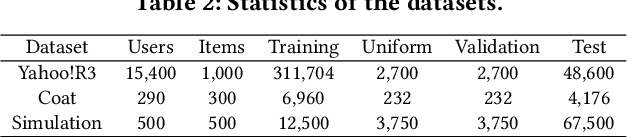
Recommender systems rely on user behavior data like ratings and clicks to build personalization model. However, the collected data is observational rather than experimental, causing various biases in the data which significantly affect the learned model. Most existing work for recommendation debiasing, such as the inverse propensity scoring and imputation approaches, focuses on one or two specific biases, lacking the universal capacity that can account for mixed or even unknown biases in the data. Towards this research gap, we first analyze the origin of biases from the perspective of \textit{risk discrepancy} that represents the difference between the expectation empirical risk and the true risk. Remarkably, we derive a general learning framework that well summarizes most existing debiasing strategies by specifying some parameters of the general framework. This provides a valuable opportunity to develop a universal solution for debiasing, e.g., by learning the debiasing parameters from data. However, the training data lacks important signal of how the data is biased and what the unbiased data looks like. To move this idea forward, we propose \textit{AotoDebias} that leverages another (small) set of uniform data to optimize the debiasing parameters by solving the bi-level optimization problem with meta-learning. Through theoretical analyses, we derive the generalization bound for AutoDebias and prove its ability to acquire the appropriate debiasing strategy. Extensive experiments on two real datasets and a simulated dataset demonstrated effectiveness of AutoDebias. The code is available at \url{https://github.com/DongHande/AutoDebias}.

On the Equivalence of Decoupled Graph Convolution Network and Label Propagation

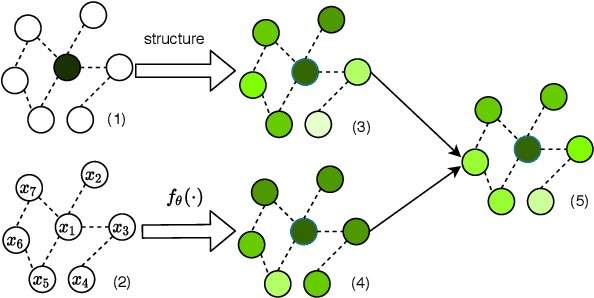
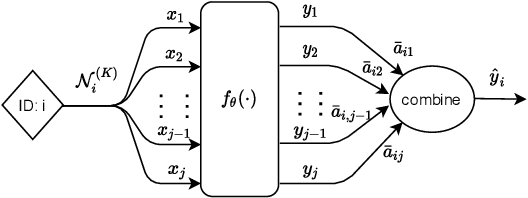
The original design of Graph Convolution Network (GCN) couples feature transformation and neighborhood aggregation for node representation learning. Recently, some work shows that coupling is inferior to decoupling, which supports deep graph propagation and has become the latest paradigm of GCN (e.g., APPNP and SGCN). Despite effectiveness, the working mechanisms of the decoupled GCN are not well understood. In this paper, we explore the decoupled GCN for semi-supervised node classification from a novel and fundamental perspective -- label propagation. We conduct thorough theoretical analyses, proving that the decoupled GCN is essentially the same as the two-step label propagation: first, propagating the known labels along the graph to generate pseudo-labels for the unlabeled nodes, and second, training normal neural network classifiers on the augmented pseudo-labeled data. More interestingly, we reveal the effectiveness of decoupled GCN: going beyond the conventional label propagation, it could automatically assign structure- and model- aware weights to the pseudo-label data. This explains why the decoupled GCN is relatively robust to the structure noise and over-smoothing, but sensitive to the label noise and model initialization. Based on this insight, we propose a new label propagation method named Propagation then Training Adaptively (PTA), which overcomes the flaws of the decoupled GCN with a dynamic and adaptive weighting strategy. Our PTA is simple yet more effective and robust than decoupled GCN. We empirically validate our findings on four benchmark datasets, demonstrating the advantages of our method.

Data Augmentation View on Graph Convolutional Network and the Proposal of Monte Carlo Graph Learning

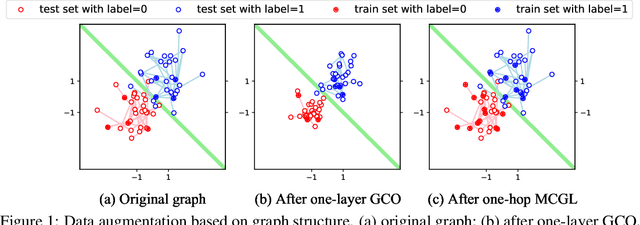
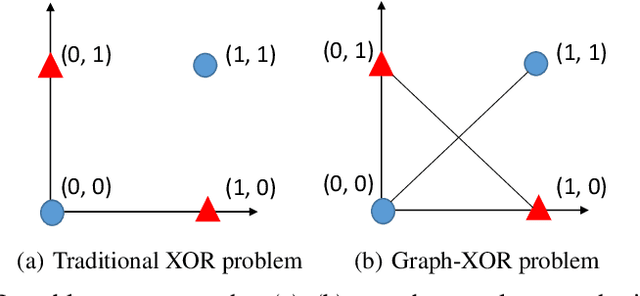
Today, there are two major understandings for graph convolutional networks, i.e., in the spectral and spatial domain. But both lack transparency. In this work, we introduce a new understanding for it -- data augmentation, which is more transparent than the previous understandings. Inspired by it, we propose a new graph learning paradigm -- Monte Carlo Graph Learning (MCGL). The core idea of MCGL contains: (1) Data augmentation: propagate the labels of the training set through the graph structure and expand the training set; (2) Model training: use the expanded training set to train traditional classifiers. We use synthetic datasets to compare the strengths of MCGL and graph convolutional operation on clean graphs. In addition, we show that MCGL's tolerance to graph structure noise is weaker than GCN on noisy graphs (four real-world datasets). Moreover, inspired by MCGL, we re-analyze the reasons why the performance of GCN becomes worse when deepened too much: rather than the mainstream view of over-smoothing, we argue that the main reason is the graph structure noise, and experimentally verify our view. The code is available at https://github.com/DongHande/MCGL.