Zhaolin Ding
On the Equivalence of Decoupled Graph Convolution Network and Label Propagation
Oct 23, 2020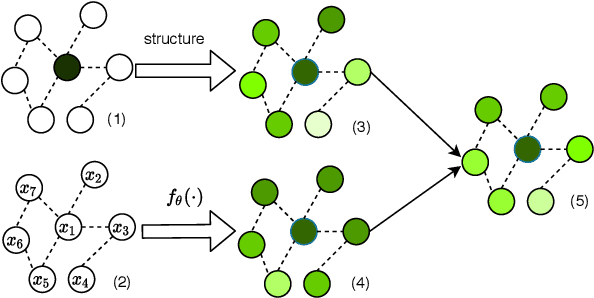

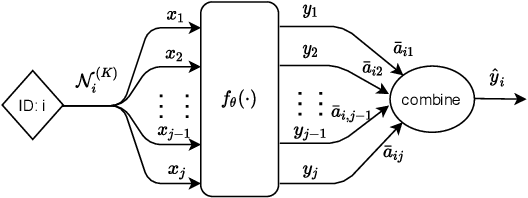
Abstract:The original design of Graph Convolution Network (GCN) couples feature transformation and neighborhood aggregation for node representation learning. Recently, some work shows that coupling is inferior to decoupling, which supports deep graph propagation and has become the latest paradigm of GCN (e.g., APPNP and SGCN). Despite effectiveness, the working mechanisms of the decoupled GCN are not well understood. In this paper, we explore the decoupled GCN for semi-supervised node classification from a novel and fundamental perspective -- label propagation. We conduct thorough theoretical analyses, proving that the decoupled GCN is essentially the same as the two-step label propagation: first, propagating the known labels along the graph to generate pseudo-labels for the unlabeled nodes, and second, training normal neural network classifiers on the augmented pseudo-labeled data. More interestingly, we reveal the effectiveness of decoupled GCN: going beyond the conventional label propagation, it could automatically assign structure- and model- aware weights to the pseudo-label data. This explains why the decoupled GCN is relatively robust to the structure noise and over-smoothing, but sensitive to the label noise and model initialization. Based on this insight, we propose a new label propagation method named Propagation then Training Adaptively (PTA), which overcomes the flaws of the decoupled GCN with a dynamic and adaptive weighting strategy. Our PTA is simple yet more effective and robust than decoupled GCN. We empirically validate our findings on four benchmark datasets, demonstrating the advantages of our method.
Data Augmentation View on Graph Convolutional Network and the Proposal of Monte Carlo Graph Learning
Jun 23, 2020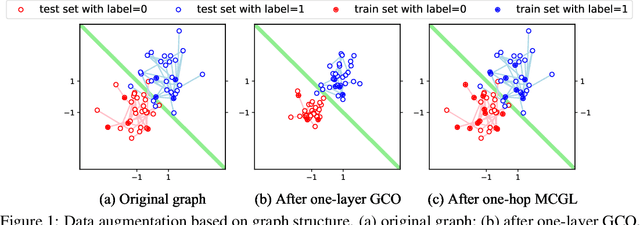


Abstract:Today, there are two major understandings for graph convolutional networks, i.e., in the spectral and spatial domain. But both lack transparency. In this work, we introduce a new understanding for it -- data augmentation, which is more transparent than the previous understandings. Inspired by it, we propose a new graph learning paradigm -- Monte Carlo Graph Learning (MCGL). The core idea of MCGL contains: (1) Data augmentation: propagate the labels of the training set through the graph structure and expand the training set; (2) Model training: use the expanded training set to train traditional classifiers. We use synthetic datasets to compare the strengths of MCGL and graph convolutional operation on clean graphs. In addition, we show that MCGL's tolerance to graph structure noise is weaker than GCN on noisy graphs (four real-world datasets). Moreover, inspired by MCGL, we re-analyze the reasons why the performance of GCN becomes worse when deepened too much: rather than the mainstream view of over-smoothing, we argue that the main reason is the graph structure noise, and experimentally verify our view. The code is available at https://github.com/DongHande/MCGL.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge