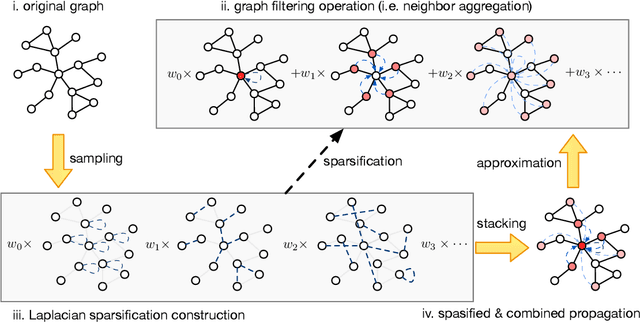
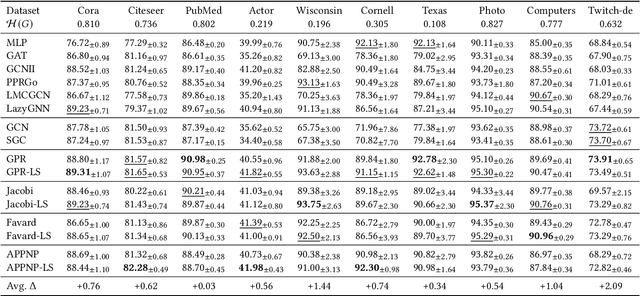
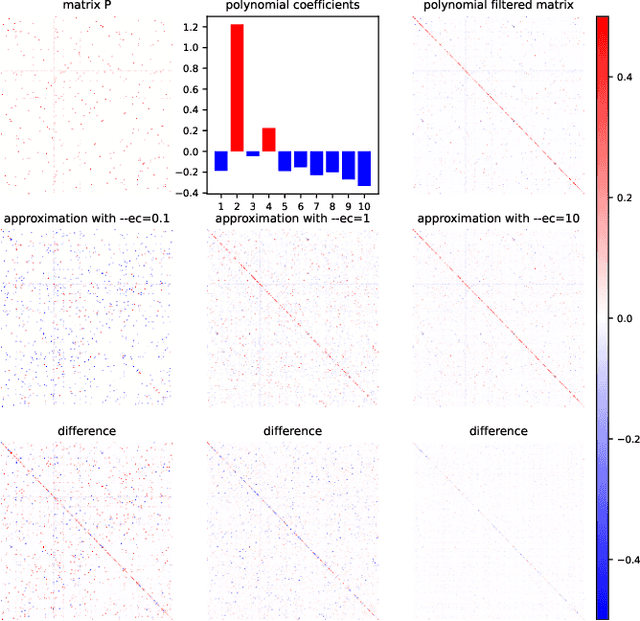
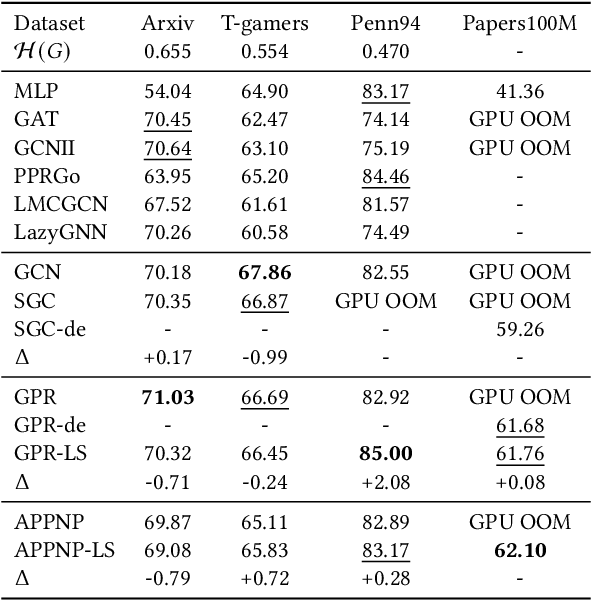
Large-Scale Spectral Graph Neural Networks via Laplacian Sparsification: Technical Report

Graph Neural Networks (GNNs) play a pivotal role in graph-based tasks for their proficiency in representation learning. Among the various GNN methods, spectral GNNs employing polynomial filters have shown promising performance on tasks involving both homophilous and heterophilous graph structures. However, The scalability of spectral GNNs on large graphs is limited because they learn the polynomial coefficients through multiple forward propagation executions during forward propagation. Existing works have attempted to scale up spectral GNNs by eliminating the linear layers on the input node features, a change that can disrupt end-to-end training, potentially impact performance, and become impractical with high-dimensional input features. To address the above challenges, we propose "Spectral Graph Neural Networks with Laplacian Sparsification (SGNN-LS)", a novel graph spectral sparsification method to approximate the propagation patterns of spectral GNNs. We prove that our proposed method generates Laplacian sparsifiers that can approximate both fixed and learnable polynomial filters with theoretical guarantees. Our method allows the application of linear layers on the input node features, enabling end-to-end training as well as the handling of raw text features. We conduct an extensive experimental analysis on datasets spanning various graph scales and properties to demonstrate the superior efficiency and effectiveness of our method. The results show that our method yields superior results in comparison with the corresponding approximated base models, especially on dataset Ogbn-papers100M(111M nodes, 1.6B edges) and MAG-scholar-C (2.8M features).

Neural-Symbolic Reasoning on Knowledge Graphs

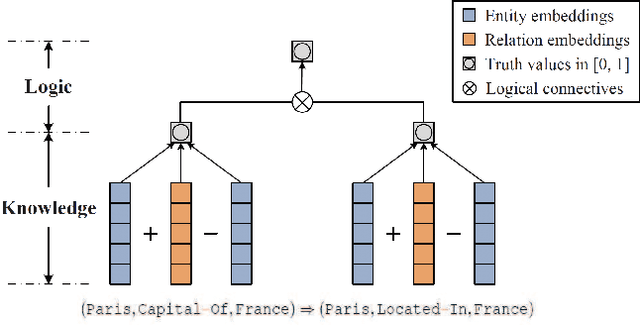
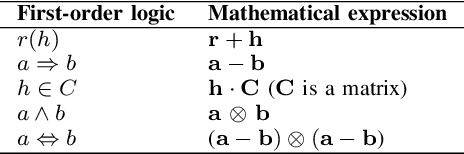
Knowledge graph reasoning is the fundamental component to support machine learning applications such as information extraction, information retrieval and recommendation. Since knowledge graph can be viewed as the discrete symbolic representations of knowledge, reasoning on knowledge graphs can naturally leverage the symbolic techniques. However, symbolic reasoning is intolerant of the ambiguous and noisy data. On the contrary, the recent advances of deep learning promote neural reasoning on knowledge graphs, which is robust to the ambiguous and noisy data, but lacks interpretability compared to symbolic reasoning. Considering the advantages and disadvantages of both methodologies, recent efforts have been made on combining the two reasoning methods. In this survey, we take a thorough look at the development of the symbolic reasoning, neural reasoning and the neural-symbolic reasoning on knowledge graphs. We survey two specific reasoning tasks, knowledge graph completion and question answering on knowledge graphs, and explain them in a unified reasoning framework. We also briefly discuss the future directions for knowledge graph reasoning.