AutoRefine: From Trajectories to Reusable Expertise for Continual LLM Agent Refinement

Large language model agents often fail to accumulate knowledge from experience, treating each task as an independent challenge. Recent methods extract experience as flattened textual knowledge, which cannot capture procedural logic of complex subtasks. They also lack maintenance mechanisms, causing repository degradation as experience accumulates. We introduce AutoRefine, a framework that extracts and maintains dual-form Experience Patterns from agent execution histories. For procedural subtasks, we extract specialized subagents with independent reasoning and memory. For static knowledge, we extract skill patterns as guidelines or code snippets. A continuous maintenance mechanism scores, prunes, and merges patterns to prevent repository degradation. Evaluated on ALFWorld, ScienceWorld, and TravelPlanner, AutoRefine achieves 98.4%, 70.4%, and 27.1% respectively, with 20-73% step reductions. On TravelPlanner, automatic extraction exceeds manually designed systems (27.1% vs 12.1%), demonstrating its ability to capture procedural coordination.

Future Link Prediction Without Memory or Aggregation

Future link prediction on temporal graphs is a fundamental task with wide applicability in real-world dynamic systems. These scenarios often involve both recurring (seen) and novel (unseen) interactions, requiring models to generalize effectively across both types of edges. However, existing methods typically rely on complex memory and aggregation modules, yet struggle to handle unseen edges. In this paper, we revisit the architecture of existing temporal graph models and identify two essential but overlooked modeling requirements for future link prediction: representing nodes with unique identifiers and performing target-aware matching between source and destination nodes. To this end, we propose Cross-Attention based Future Link Predictor on Temporal Graphs (CRAFT), a simple yet effective architecture that discards memory and aggregation modules and instead builds on two components: learnable node embeddings and cross-attention between the destination and the source's recent interactions. This design provides strong expressive power and enables target-aware modeling of the compatibility between candidate destinations and the source's interaction patterns. Extensive experiments on diverse datasets demonstrate that CRAFT consistently achieves superior performance with high efficiency, making it well-suited for large-scale real-world applications.

TGB-Seq Benchmark: Challenging Temporal GNNs with Complex Sequential Dynamics

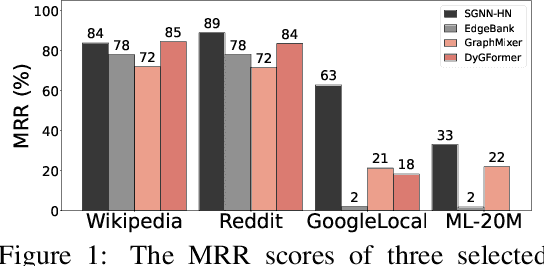
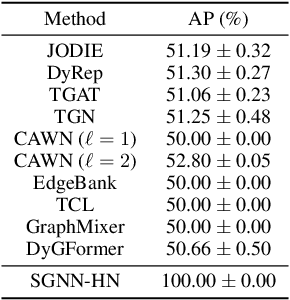
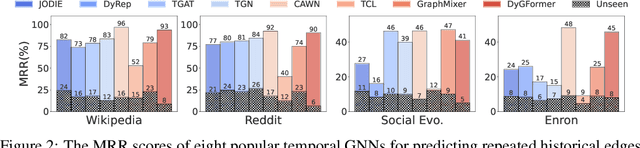
Future link prediction is a fundamental challenge in various real-world dynamic systems. To address this, numerous temporal graph neural networks (temporal GNNs) and benchmark datasets have been developed. However, these datasets often feature excessive repeated edges and lack complex sequential dynamics, a key characteristic inherent in many real-world applications such as recommender systems and ``Who-To-Follow'' on social networks. This oversight has led existing methods to inadvertently downplay the importance of learning sequential dynamics, focusing primarily on predicting repeated edges. In this study, we demonstrate that existing methods, such as GraphMixer and DyGFormer, are inherently incapable of learning simple sequential dynamics, such as ``a user who has followed OpenAI and Anthropic is more likely to follow AI at Meta next.'' Motivated by this issue, we introduce the Temporal Graph Benchmark with Sequential Dynamics (TGB-Seq), a new benchmark carefully curated to minimize repeated edges, challenging models to learn sequential dynamics and generalize to unseen edges. TGB-Seq comprises large real-world datasets spanning diverse domains, including e-commerce interactions, movie ratings, business reviews, social networks, citation networks and web link networks. Benchmarking experiments reveal that current methods usually suffer significant performance degradation and incur substantial training costs on TGB-Seq, posing new challenges and opportunities for future research. TGB-Seq datasets, leaderboards, and example codes are available at https://tgb-seq.github.io/.

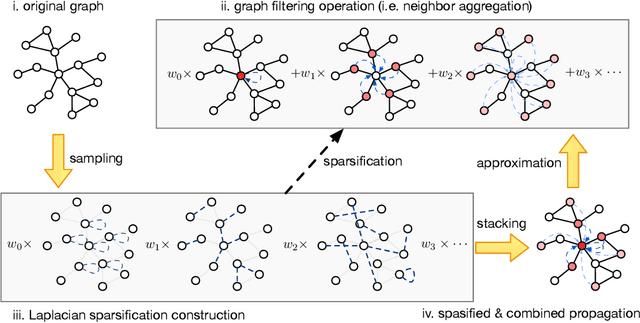
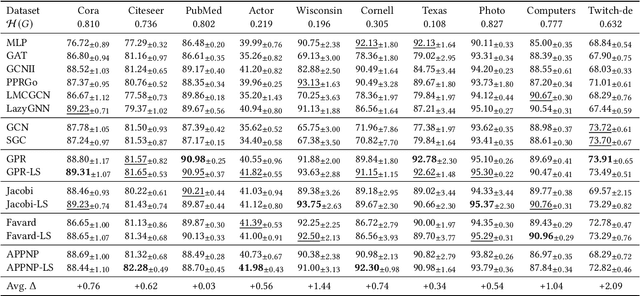
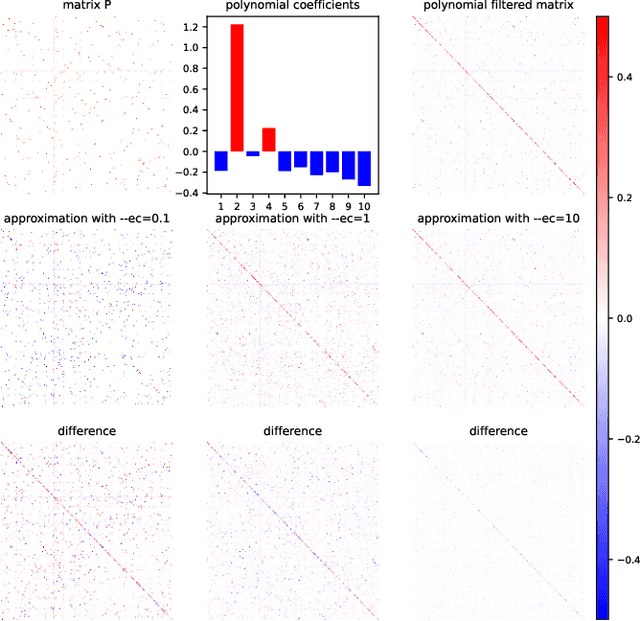
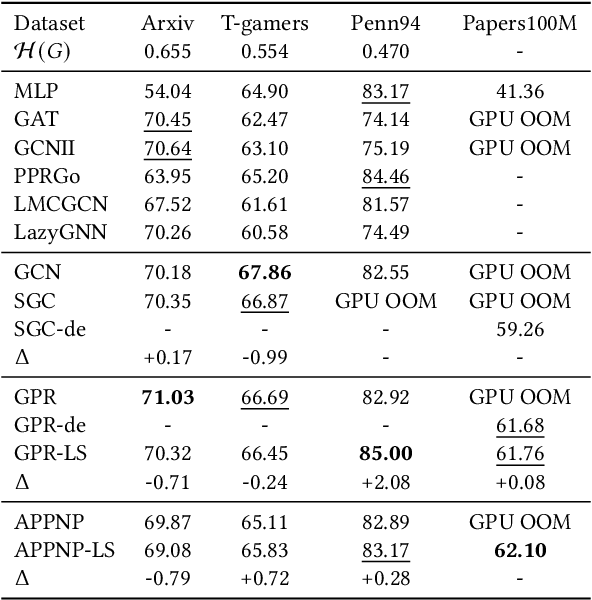
Large-Scale Spectral Graph Neural Networks via Laplacian Sparsification: Technical Report

Graph Neural Networks (GNNs) play a pivotal role in graph-based tasks for their proficiency in representation learning. Among the various GNN methods, spectral GNNs employing polynomial filters have shown promising performance on tasks involving both homophilous and heterophilous graph structures. However, The scalability of spectral GNNs on large graphs is limited because they learn the polynomial coefficients through multiple forward propagation executions during forward propagation. Existing works have attempted to scale up spectral GNNs by eliminating the linear layers on the input node features, a change that can disrupt end-to-end training, potentially impact performance, and become impractical with high-dimensional input features. To address the above challenges, we propose "Spectral Graph Neural Networks with Laplacian Sparsification (SGNN-LS)", a novel graph spectral sparsification method to approximate the propagation patterns of spectral GNNs. We prove that our proposed method generates Laplacian sparsifiers that can approximate both fixed and learnable polynomial filters with theoretical guarantees. Our method allows the application of linear layers on the input node features, enabling end-to-end training as well as the handling of raw text features. We conduct an extensive experimental analysis on datasets spanning various graph scales and properties to demonstrate the superior efficiency and effectiveness of our method. The results show that our method yields superior results in comparison with the corresponding approximated base models, especially on dataset Ogbn-papers100M(111M nodes, 1.6B edges) and MAG-scholar-C (2.8M features).