Wide Neural Networks as Gaussian Processes: Lessons from Deep Equilibrium Models

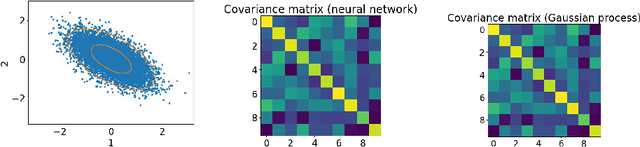
Neural networks with wide layers have attracted significant attention due to their equivalence to Gaussian processes, enabling perfect fitting of training data while maintaining generalization performance, known as benign overfitting. However, existing results mainly focus on shallow or finite-depth networks, necessitating a comprehensive analysis of wide neural networks with infinite-depth layers, such as neural ordinary differential equations (ODEs) and deep equilibrium models (DEQs). In this paper, we specifically investigate the deep equilibrium model (DEQ), an infinite-depth neural network with shared weight matrices across layers. Our analysis reveals that as the width of DEQ layers approaches infinity, it converges to a Gaussian process, establishing what is known as the Neural Network and Gaussian Process (NNGP) correspondence. Remarkably, this convergence holds even when the limits of depth and width are interchanged, which is not observed in typical infinite-depth Multilayer Perceptron (MLP) networks. Furthermore, we demonstrate that the associated Gaussian vector remains non-degenerate for any pairwise distinct input data, ensuring a strictly positive smallest eigenvalue of the corresponding kernel matrix using the NNGP kernel. These findings serve as fundamental elements for studying the training and generalization of DEQs, laying the groundwork for future research in this area.

SGEM: stochastic gradient with energy and momentum

In this paper, we propose SGEM, Stochastic Gradient with Energy and Momentum, to solve a large class of general non-convex stochastic optimization problems, based on the AEGD method that originated in the work [AEGD: Adaptive Gradient Descent with Energy. arXiv: 2010.05109]. SGEM incorporates both energy and momentum at the same time so as to inherit their dual advantages. We show that SGEM features an unconditional energy stability property, and derive energy-dependent convergence rates in the general nonconvex stochastic setting, as well as a regret bound in the online convex setting. A lower threshold for the energy variable is also provided. Our experimental results show that SGEM converges faster than AEGD and generalizes better or at least as well as SGDM in training some deep neural networks.

An Adaptive Gradient Method with Energy and Momentum

We introduce a novel algorithm for gradient-based optimization of stochastic objective functions. The method may be seen as a variant of SGD with momentum equipped with an adaptive learning rate automatically adjusted by an 'energy' variable. The method is simple to implement, computationally efficient, and well suited for large-scale machine learning problems. The method exhibits unconditional energy stability for any size of the base learning rate. We provide a regret bound on the convergence rate under the online convex optimization framework. We also establish the energy-dependent convergence rate of the algorithm to a stationary point in the stochastic non-convex setting. In addition, a sufficient condition is provided to guarantee a positive lower threshold for the energy variable. Our experiments demonstrate that the algorithm converges fast while generalizing better than or as well as SGD with momentum in training deep neural networks, and compares also favorably to Adam.

A global convergence theory for deep ReLU implicit networks via over-parameterization

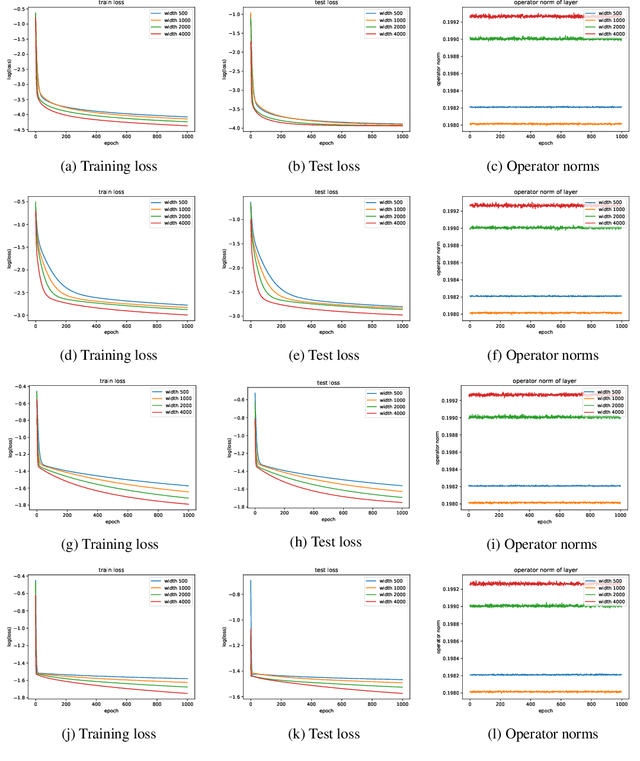
Implicit deep learning has received increasing attention recently due to the fact that it generalizes the recursive prediction rules of many commonly used neural network architectures. Its prediction rule is provided implicitly based on the solution of an equilibrium equation. Although a line of recent empirical studies has demonstrated its superior performances, the theoretical understanding of implicit neural networks is limited. In general, the equilibrium equation may not be well-posed during the training. As a result, there is no guarantee that a vanilla (stochastic) gradient descent (SGD) training nonlinear implicit neural networks can converge. This paper fills the gap by analyzing the gradient flow of Rectified Linear Unit (ReLU) activated implicit neural networks. For an $m$-width implicit neural network with ReLU activation and $n$ training samples, we show that a randomly initialized gradient descent converges to a global minimum at a linear rate for the square loss function if the implicit neural network is \textit{over-parameterized}. It is worth noting that, unlike existing works on the convergence of (S)GD on finite-layer over-parameterized neural networks, our convergence results hold for implicit neural networks, where the number of layers is \textit{infinite}.

AEGD: Adaptive Gradient Decent with Energy

In this paper, we propose AEGD, a new algorithm for first-order gradient-based optimization of stochastic objective functions, based on adaptive updates of quadratic energy. As long as an objective function is bounded from below, AEGD can be applied, and it is shown to be unconditionally energy stable, irrespective of the step size. In addition, AEGD enjoys tight convergence rates, yet allows a large step size. The method is straightforward to implement and requires little tuning of hyper-parameters. Experimental results demonstrate that AEGD works well for various optimization problems: it is robust with respect to initial data, capable of making rapid initial progress, shows comparable and most times better generalization performance than SGD with momentum for deep neural networks. The implementation of the algorithm can be found at https://github.com/txping/AEGD.