Wide Neural Networks as Gaussian Processes: Lessons from Deep Equilibrium Models
Paper and Code
Oct 16, 2023
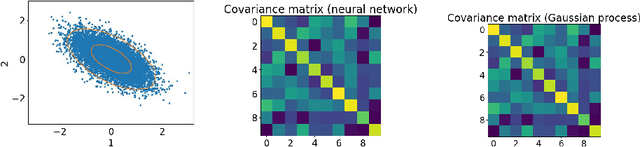


Neural networks with wide layers have attracted significant attention due to their equivalence to Gaussian processes, enabling perfect fitting of training data while maintaining generalization performance, known as benign overfitting. However, existing results mainly focus on shallow or finite-depth networks, necessitating a comprehensive analysis of wide neural networks with infinite-depth layers, such as neural ordinary differential equations (ODEs) and deep equilibrium models (DEQs). In this paper, we specifically investigate the deep equilibrium model (DEQ), an infinite-depth neural network with shared weight matrices across layers. Our analysis reveals that as the width of DEQ layers approaches infinity, it converges to a Gaussian process, establishing what is known as the Neural Network and Gaussian Process (NNGP) correspondence. Remarkably, this convergence holds even when the limits of depth and width are interchanged, which is not observed in typical infinite-depth Multilayer Perceptron (MLP) networks. Furthermore, we demonstrate that the associated Gaussian vector remains non-degenerate for any pairwise distinct input data, ensuring a strictly positive smallest eigenvalue of the corresponding kernel matrix using the NNGP kernel. These findings serve as fundamental elements for studying the training and generalization of DEQs, laying the groundwork for future research in this area.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge