An Operator Theory for Analyzing the Resolution of Multi-illumination Imaging Modalities

By introducing a new operator theory, we provide a unified mathematical theory for general source resolution in the multi-illumination imaging problem. Our main idea is to transform multi-illumination imaging into single-snapshot imaging with a new imaging kernel that depends on both the illumination patterns and the point spread function of the imaging system. We thus prove that the resolution of multi-illumination imaging is approximately determined by the essential cutoff frequency of the new imaging kernel, which is roughly limited by the sum of the cutoff frequency of the point spread function and the maximum essential frequency in the illumination patterns. Our theory provides a unified way to estimate the resolution of various existing super-resolution modalities and results in the same estimates as those obtained in experiments. In addition, based on the reformulation of the multi-illumination imaging problem, we also estimate the resolution limits for resolving both complex and positive sources by sparsity-based approaches. We show that the resolution of multi-illumination imaging is approximately determined by the new imaging kernel from our operator theory and better resolution can be realized by sparsity-promoting techniques in practice but only for resolving very sparse sources. This explains experimentally observed phenomena in some sparsity-based super-resolution modalities.

Super-resolution of positive near-colliding point sources

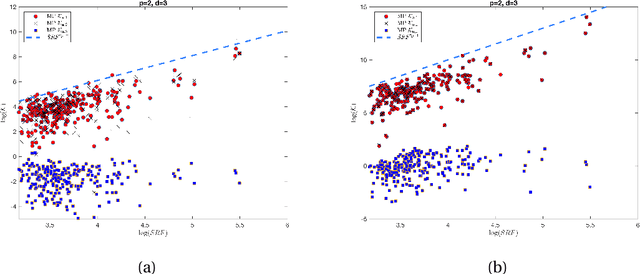
In this paper, we analyze the capacity of super-resolution of one-dimensional positive sources. In particular, we consider the same setting as in [arXiv:1904.09186v2 [math.NA]] and generalize the results there to the case of super-resolving positive sources. To be more specific, we consider resolving $d$ positive point sources with $p \leqslant d$ nodes closely spaced and forming a cluster, while the rest of the nodes are well separated. Similarly to [arXiv:1904.09186v2 [math.NA]], our results show that when the noise level $\epsilon \lesssim \mathrm{SRF}^{-2 p+1}$, where $\mathrm{SRF}=(\Omega \Delta)^{-1}$ with $\Omega$ being the cutoff frequency and $\Delta$ the minimal separation between the nodes, the minimax error rate for reconstructing the cluster nodes is of order $\frac{1}{\Omega} \mathrm{SRF}^{2 p-2} \epsilon$, while for recovering the corresponding amplitudes $\left\{a_j\right\}$ the rate is of order $\mathrm{SRF}^{2 p-1} \epsilon$. For the non-cluster nodes, the corresponding minimax rates for the recovery of nodes and amplitudes are of order $\frac{\epsilon}{\Omega}$ and $\epsilon$, respectively. Our numerical experiments show that the Matrix Pencil method achieves the above optimal bounds when resolving the positive sources.

A mathematical theory of super-resolution and diffraction limit

This paper is devoted to elucidating the essence of super-resolution and deals mainly with the stability of super-resolution and the diffraction limit. The first discovery is two location-amplitude identities characterizing the relations between source locations and amplitudes in the super-resolution problem. These identities allow us to directly derive the super-resolution capability for number, location, and amplitude recovery in the super-resolution problem and improve state-of-the-art estimations to an unprecedented level to have practical significance. The nonlinear inverse problems studied in this paper are known to be very challenging and have only been partially solved in recent years, but we now have a clear and simple picture of all of these problems, which allows us to solve them in a unified way in just a few pages. The second crucial result of this paper is the theoretical proof of a two-point diffraction limit in spaces of general dimensionality under only an assumption on the noise level. The two-point diffraction limit is given by \[ \mathcal{R} = \frac{4\arcsin \left(\left(\frac{\sigma}{m_{\min}}\right)^{\frac{1}{2}} \right)}{\Omega} \] for $\frac{\sigma}{m_{\min}}\leq\frac{1}{2}$, where $\frac{\sigma}{m_{\min}}$ represents the inverse of the signal-to-noise ratio ($SNR$) and $\Omega$ is the cutoff frequency. In the case when $\frac{\sigma}{m_{\min}}>\frac{1}{2}$, there is no super-resolution in certain cases. This solves the long-standing puzzle and debate about the diffraction limit for imaging (and line spectral estimation) in very general circumstances. Our results also show that, for the resolution of any two point sources, when $SNR>2$, one can definitely exceed the Rayleigh limit $\frac{\pi}{\Omega}$, which is far beyond common sense. We also find the optimal algorithm that achieves the optimal resolution when distinguishing two sources.

A mathematical theory of resolution limits for super-resolution of positive sources

The superresolving capacity for number and location recoveries in the super-resolution of positive sources is analyzed in this work. Specifically, we introduce the computational resolution limit for respectively the number detection and location recovery in the one-dimensional super-resolution problem and quantitatively characterize their dependency on the cutoff frequency, signal-to-noise ratio, and the sparsity of the sources. As a direct consequence, we show that targeting at the sparest positive solution in the super-resolution already provides the optimal resolution order. These results are generalized to multi-dimensional spaces. Our estimates indicate that there exist phase transitions in the corresponding reconstructions, which are confirmed by numerical experiments. Our theory fills in an important puzzle towards fully understanding the super-resolution of positive sources.

Nearly optimal resolution estimate for the two-dimensional super-resolution and a new algorithm for direction of arrival estimation with uniform rectangular array

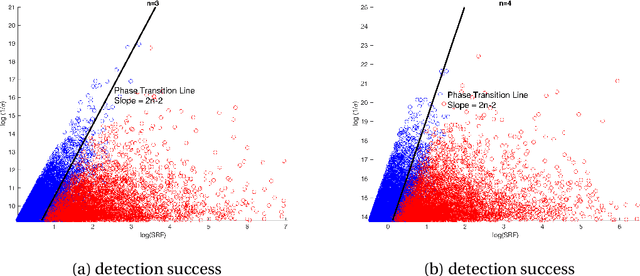
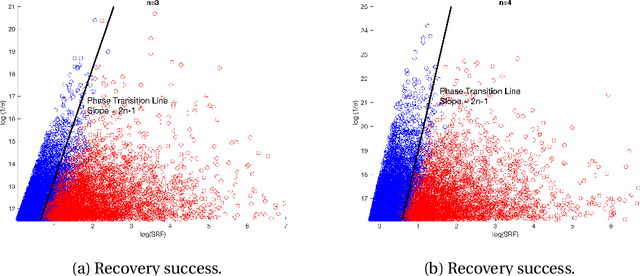
In this paper, we develop a new technique to obtain nearly optimal estimates of the computational resolution limits introduced in Appl. Comput. Harmon. Anal. 56 (2022) 402-446; IEEE Trans. Inf. Theory 67(7) (2021) 4812-4827; Inverse Probl. 37(10) (2021) 104001 for two-dimensional super-resolution problems. Our main contributions are fivefold: (i) Our work improves the resolution estimate for number detection and location recovery in two-dimensional super-resolution problems to nearly optimal; (ii) As a consequence, we derive a stability result for a sparsity-promoting algorithm in two-dimensional super-resolution problems (or Direction of Arrival problems (DOA)). The stability result exhibits the optimal performance of sparsity promoting in solving such problems; (iii) Our techniques pave the way for improving the estimate for resolution limits in higher-dimensional super-resolutions to nearly optimal; (iv) Inspired by these new techniques, we propose a new coordinate-combination-based model order detection algorithm for two-dimensional DOA estimation and theoretically demonstrate its optimal performance, and (v) we also propose a new coordinate-combination-based MUSIC algorithm for super-resolving sources in two-dimensional DOA estimation. It has excellent performance and enjoys many advantages compared to the conventional DOA algorithms. The coordinate-combination idea seems to be a promising way for multi-dimensional DOA estimation.

Dynamic super-resolution in particle tracking problems

Particle tracking in biological imaging is concerned with reconstructing the trajectories, locations, or velocities of the targeting particles. The standard approach of particle tracking consists of two steps: first reconstructing statically the source locations in each time step, and second applying tracking techniques to obtain the trajectories and velocities. In contrast, the dynamic reconstruction seeks to simultaneously recover the source locations and velocities from all frames, which enjoys certain advantages. In this paper, we provide a rigorous mathematical analysis for the resolution limit of reconstructing source number, locations, and velocities by general dynamical reconstruction in particle tracking problems, by which we demonstrate the possibility of achieving super-resolution for the dynamic reconstruction. We show that when the location-velocity pairs of the particles are separated beyond certain distances (the resolution limits), the number of particles and the location-velocity pair can be stably recovered. The resolution limits are related to the cut-off frequency of the imaging system, signal-to-noise ratio, and the sparsity of the source. By these estimates, we also derive a stability result for a sparsity-promoting dynamic reconstruction. In addition, we further show that the reconstruction of velocities has a better resolution limit which improves constantly as the particles moving. This result is derived by an observation that the inherent cut-off frequency for the velocity recovery can be viewed as the total observation time multiplies the cut-off frequency of the imaging system, which may lead to a better resolution limit as compared to the one for each diffraction-limited frame. It is anticipated that this observation can inspire new reconstruction algorithms that improve the resolution of particle tracking in practice.

Mathematical foundation of sparsity-based multi-illumination super-resolution

It is well-known that the resolution of a traditional optical imaging system is limited by the so-called Rayleigh limit, which is of several hundreds of nanometers. By employing fluorescence techniques, modern microscopic methods can resolve point scatterers separated much lower than the Rayleigh limit. Localization-based fluorescence subwavelength imaging techniques such as PALM and STORM can achieve a spatial resolution of several tens of nanometers. However, these techniques have limited temporal resolution as they require tens of thousands of exposures. Employing sparsity-based models and recovery algorithms is a natural way to reduce the number of exposures and hence obtain high temporal resolution. Recently, a new multi-illumination imaging technique called Brownian Excitation Amplitude Modulation microscopy (BEAM) is introduced. BEAM achieves a threefold resolution improvement by applying a compressive sensing recovery algorithm over only few frames. Motivated by BEAM, our aim in this paper is to pioneer the mathematical foundation for sparsity-based multi-illumination super-resolution. We consider several diffraction-limited images from samples exposed to different illumination patterns and recover the source by considering the sparsest solution. We estimate the minimum separation distance between point scatterers so that they could be stably recovered. By this estimation, we reveal the dependence of the resolution on the cut-off frequency of the imaging system, the SNR, the sparsity of point scatterers, and the incoherence of illumination patterns. Our theory particularly highlights the importance of the high incoherence of illumination patterns in enhancing the resolution. It also demonstrates that super-resolution can be achieved using sparsity-based multi-illumination imaging with very few frames, whereby the spatio-temporal super-resolution becomes possible.

Robust Cardiac Motion Estimation using Ultrafast Ultrasound Data: A Low-Rank-Topology-Preserving Approach

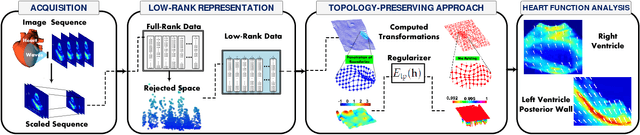
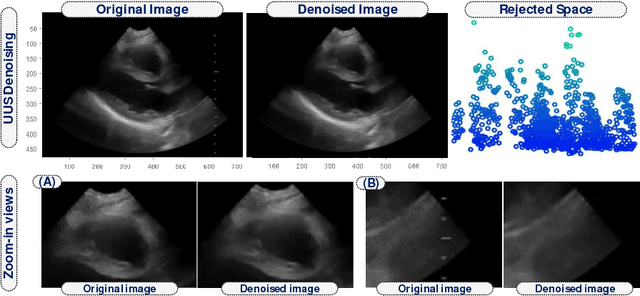
Cardiac motion estimation is an important diagnostic tool to detect heart diseases and it has been explored with modalities such as MRI and conventional ultrasound (US) sequences. US cardiac motion estimation still presents challenges because of the complex motion patterns and the presence of noise. In this work, we propose a novel approach to estimate the cardiac motion using ultrafast ultrasound data. -- Our solution is based on a variational formulation characterized by the L2-regularized class. The displacement is represented by a lattice of b-splines and we ensure robustness by applying a maximum likelihood type estimator. While this is an important part of our solution, the main highlight of this paper is to combine a low-rank data representation with topology preservation. Low-rank data representation (achieved by finding the k-dominant singular values of a Casorati Matrix arranged from the data sequence) speeds up the global solution and achieves noise reduction. On the other hand, topology preservation (achieved by monitoring the Jacobian determinant) allows to radically rule out distortions while carefully controlling the size of allowed expansions and contractions. Our variational approach is carried out on a realistic dataset as well as on a simulated one. We demonstrate how our proposed variational solution deals with complex deformations through careful numerical experiments. While maintaining the accuracy of the solution, the low-rank preprocessing is shown to speed up the convergence of the variational problem. Beyond cardiac motion estimation, our approach is promising for the analysis of other organs that experience motion.

Time-domain multiscale shape identification in electro-sensing

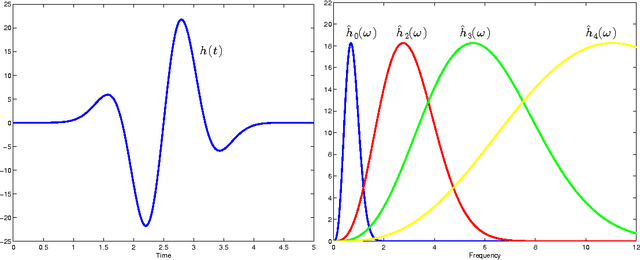
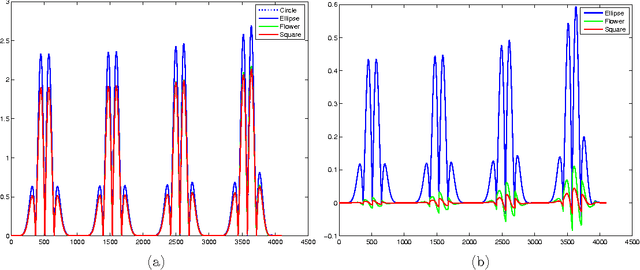
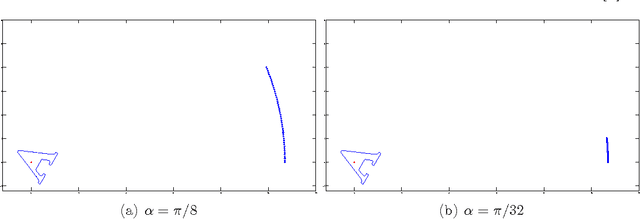
This paper presents premier and innovative time-domain multi-scale method for shape identification in electro-sensing using pulse-type signals. The method is based on transform-invariant shape descriptors computed from filtered polarization tensors at multi-scales. The proposed algorithm enjoys a remarkable noise robustness even with far-field measurements at very limited angle of view. It opens a door for pulsed imaging using echolocation and induction data.

Wavelet methods for shape perception in electro-sensing

This paper aims at presenting a new approach to the electro-sensing problem using wavelets. It provides an efficient algorithm for recognizing the shape of a target from micro-electrical impedance measurements. Stability and resolution capabilities of the proposed algorithm are quantified in numerical simulations.