Nearly optimal resolution estimate for the two-dimensional super-resolution and a new algorithm for direction of arrival estimation with uniform rectangular array
Paper and Code
May 14, 2022
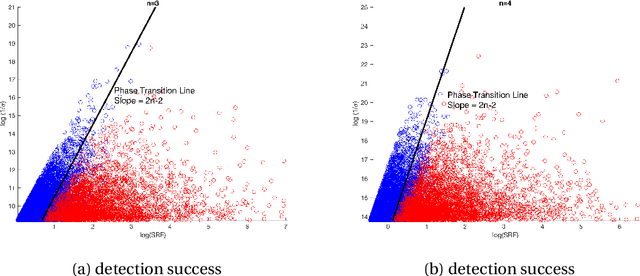

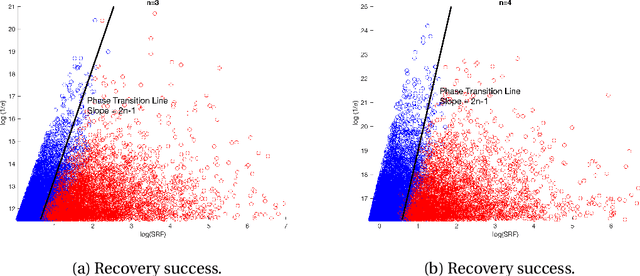
In this paper, we develop a new technique to obtain nearly optimal estimates of the computational resolution limits introduced in Appl. Comput. Harmon. Anal. 56 (2022) 402-446; IEEE Trans. Inf. Theory 67(7) (2021) 4812-4827; Inverse Probl. 37(10) (2021) 104001 for two-dimensional super-resolution problems. Our main contributions are fivefold: (i) Our work improves the resolution estimate for number detection and location recovery in two-dimensional super-resolution problems to nearly optimal; (ii) As a consequence, we derive a stability result for a sparsity-promoting algorithm in two-dimensional super-resolution problems (or Direction of Arrival problems (DOA)). The stability result exhibits the optimal performance of sparsity promoting in solving such problems; (iii) Our techniques pave the way for improving the estimate for resolution limits in higher-dimensional super-resolutions to nearly optimal; (iv) Inspired by these new techniques, we propose a new coordinate-combination-based model order detection algorithm for two-dimensional DOA estimation and theoretically demonstrate its optimal performance, and (v) we also propose a new coordinate-combination-based MUSIC algorithm for super-resolving sources in two-dimensional DOA estimation. It has excellent performance and enjoys many advantages compared to the conventional DOA algorithms. The coordinate-combination idea seems to be a promising way for multi-dimensional DOA estimation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge