Cooperative Control of Mobile Robots with Stackelberg Learning

Multi-robot cooperation requires agents to make decisions that are consistent with the shared goal without disregarding action-specific preferences that might arise from asymmetry in capabilities and individual objectives. To accomplish this goal, we propose a method named SLiCC: Stackelberg Learning in Cooperative Control. SLiCC models the problem as a partially observable stochastic game composed of Stackelberg bimatrix games, and uses deep reinforcement learning to obtain the payoff matrices associated with these games. Appropriate cooperative actions are then selected with the derived Stackelberg equilibria. Using a bi-robot cooperative object transportation problem, we validate the performance of SLiCC against centralized multi-agent Q-learning and demonstrate that SLiCC achieves better combined utility.

Distributed Reinforcement Learning for Cooperative Multi-Robot Object Manipulation

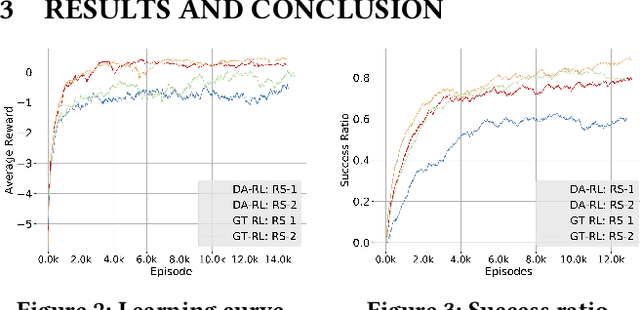
We consider solving a cooperative multi-robot object manipulation task using reinforcement learning (RL). We propose two distributed multi-agent RL approaches: distributed approximate RL (DA-RL), where each agent applies Q-learning with individual reward functions; and game-theoretic RL (GT-RL), where the agents update their Q-values based on the Nash equilibrium of a bimatrix Q-value game. We validate the proposed approaches in the setting of cooperative object manipulation with two simulated robot arms. Although we focus on a small system of two agents in this paper, both DA-RL and GT-RL apply to general multi-agent systems, and are expected to scale well to large systems.

Towards Scalable Koopman Operator Learning: Convergence Rates and A Distributed Learning Algorithm

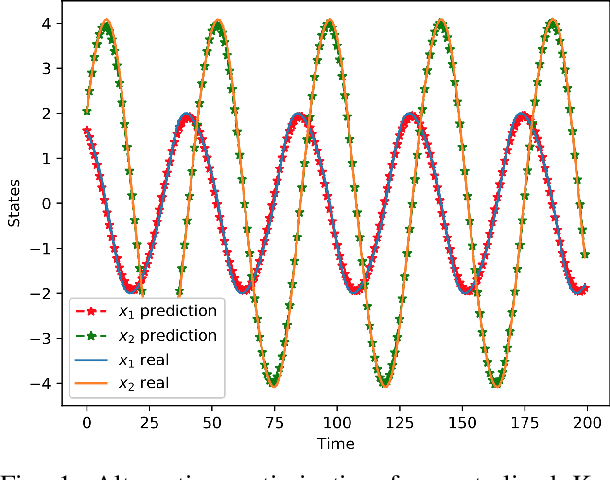
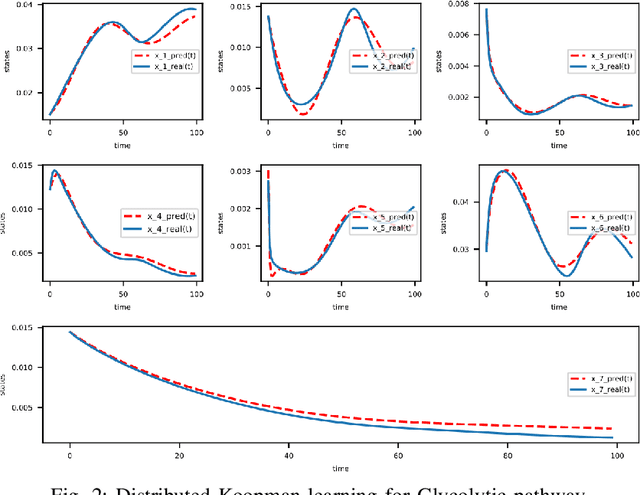
In this paper, we propose an alternating optimization algorithm to the nonconvex Koopman operator learning problem for nonlinear dynamic systems. We show that the proposed algorithm will converge to a critical point with rate $O(1/T)$ or $O(\frac{1}{\log T})$ under some mild assumptions. To handle the high dimensional nonlinear dynamical systems, we present the first-ever distributed Koopman operator learning algorithm. We show that the distributed Koopman operator learning has the same convergence properties as a centralized Koopman operator learning problem, in the absence of optimal tracker, so long as the basis functions satisfy a set of state-based decomposition conditions. Experiments are provided to complement our theoretical results.