Towards Scalable Koopman Operator Learning: Convergence Rates and A Distributed Learning Algorithm
Paper and Code
Sep 30, 2019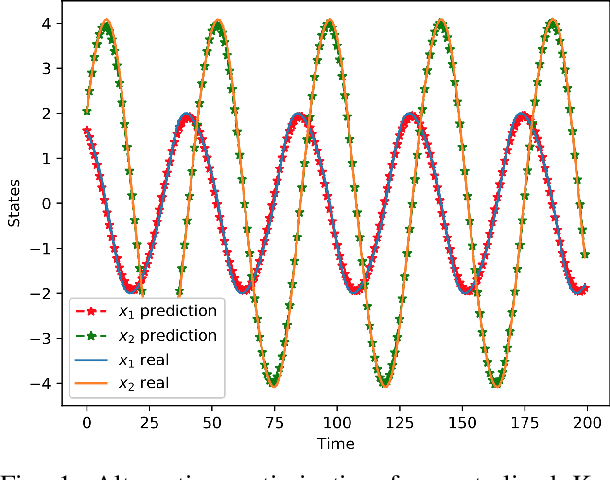
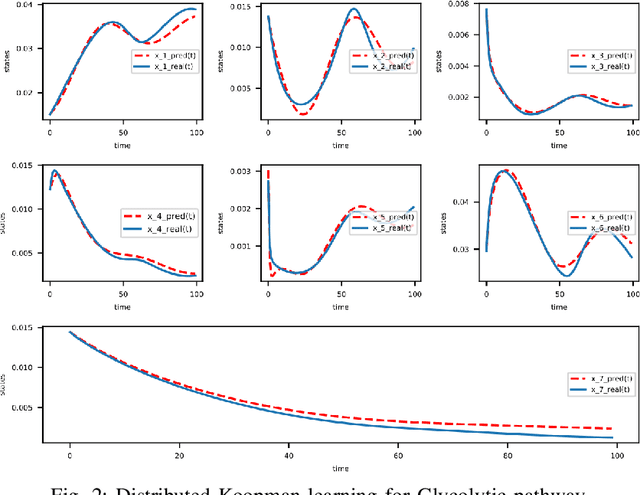
In this paper, we propose an alternating optimization algorithm to the nonconvex Koopman operator learning problem for nonlinear dynamic systems. We show that the proposed algorithm will converge to a critical point with rate $O(1/T)$ or $O(\frac{1}{\log T})$ under some mild assumptions. To handle the high dimensional nonlinear dynamical systems, we present the first-ever distributed Koopman operator learning algorithm. We show that the distributed Koopman operator learning has the same convergence properties as a centralized Koopman operator learning problem, in the absence of optimal tracker, so long as the basis functions satisfy a set of state-based decomposition conditions. Experiments are provided to complement our theoretical results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge