Guo-Yong Xiang
On compression rate of quantum autoencoders: Control design, numerical and experimental realization
May 22, 2020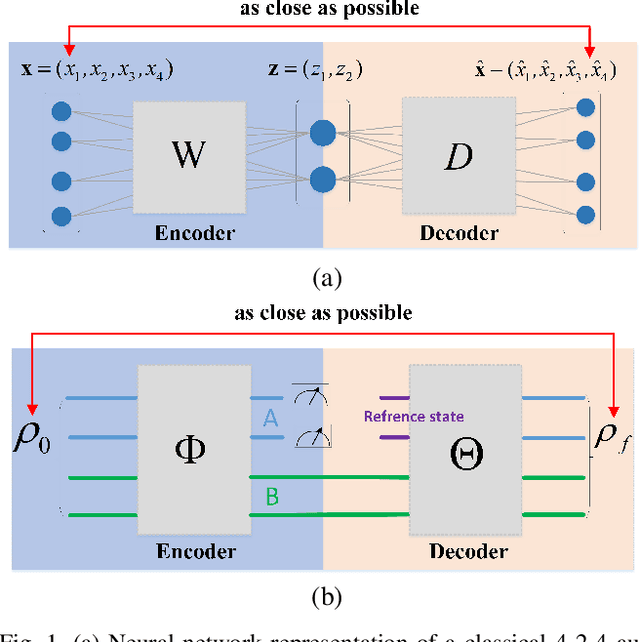
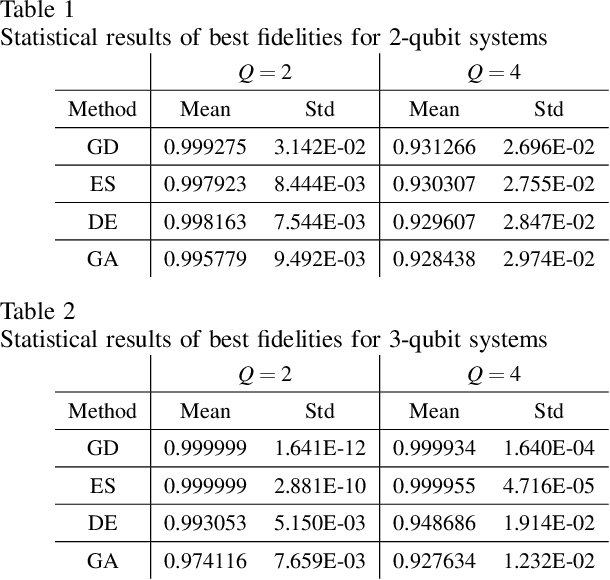
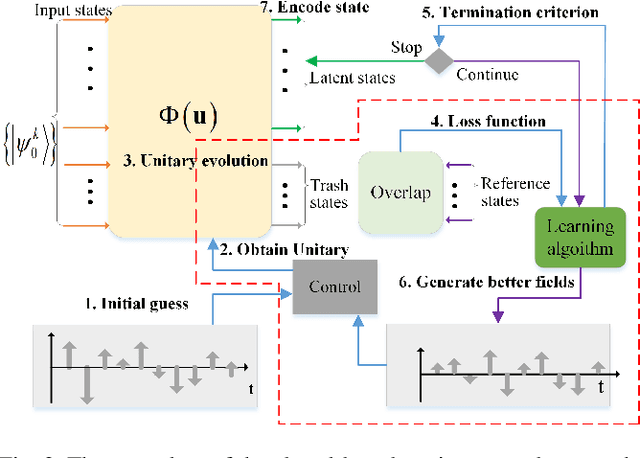
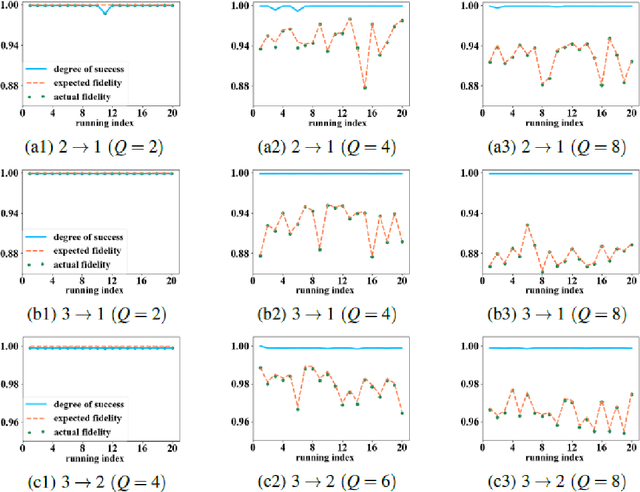
Abstract:Quantum autoencoders which aim at compressing quantum information in a low-dimensional latent space lie in the heart of automatic data compression in the field of quantum information. In this paper, we establish an upper bound of the compression rate for a given quantum autoencoder and present a learning control approach for training the autoencoder to achieve the maximal compression rate. The upper bound of the compression rate is theoretically proven using eigen-decomposition and matrix differentiation, which is determined by the eigenvalues of the density matrix representation of the input states. Numerical results on 2-qubit and 3-qubit systems are presented to demonstrate how to train the quantum autoencoder to achieve the theoretically maximal compression, and the training performance using different machine learning algorithms is compared. Experimental results of a quantum autoencoder using quantum optical systems are illustrated for compressing two 2-qubit states into two 1-qubit states.
Experimentally detecting a quantum change point via Bayesian inference
Jan 23, 2018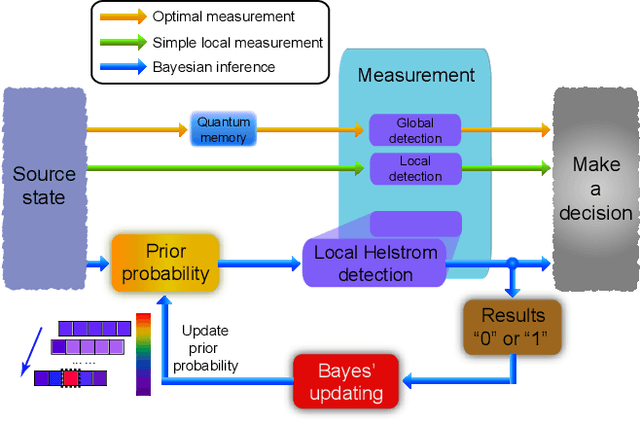
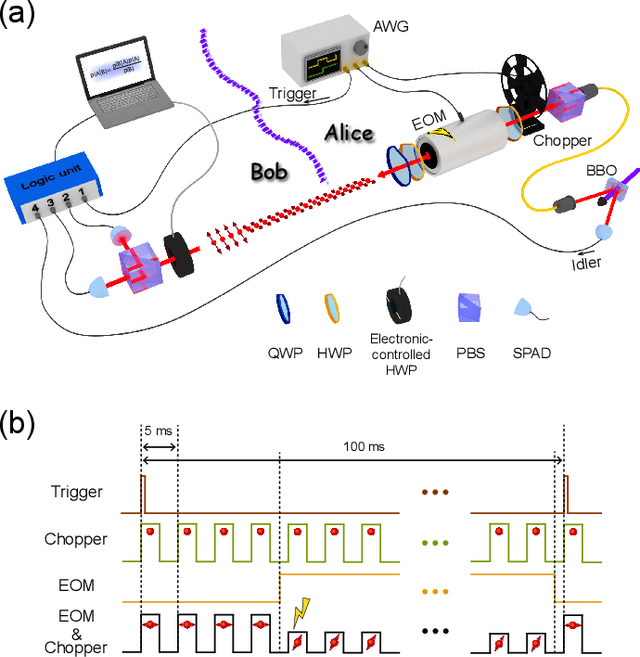
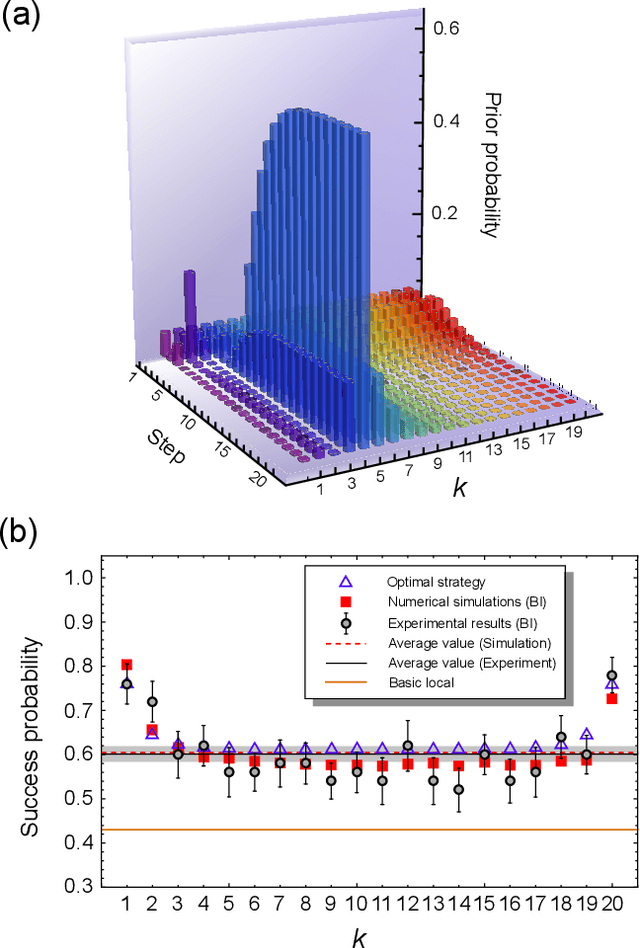
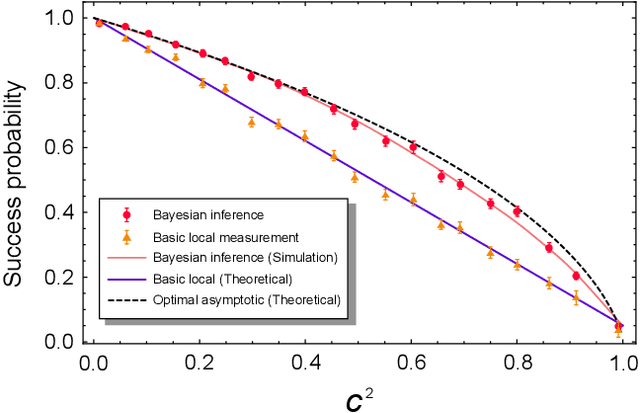
Abstract:Detecting a change point is a crucial task in statistics that has been recently extended to the quantum realm. A source state generator that emits a series of single photons in a default state suffers an alteration at some point and starts to emit photons in a mutated state. The problem consists in identifying the point where the change took place. In this work, we consider a learning agent that applies Bayesian inference on experimental data to solve this problem. This learning machine adjusts the measurement over each photon according to the past experimental results finds the change position in an online fashion. Our results show that the local-detection success probability can be largely improved by using such a machine learning technique. This protocol provides a tool for improvement in many applications where a sequence of identical quantum states is required.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge