Unleashing the Expressive Power of Pulse-Based Quantum Neural Networks

Quantum machine learning (QML) based on Noisy Intermediate-Scale Quantum (NISQ) devices requires the optimal utilization of limited quantum resources. The commonly used gate-based QML models are convenient for software engineers, but their expressivity is restricted by the permissible circuit depth within a finite coherence time. In contrast, pulse-based models enable the construction of "infinitely" deep quantum neural networks within the same coherence time, which may unleash greater expressive power for complex learning tasks. In this paper, we investigate this potential from the perspective of quantum control theory. We first indicate that the nonlinearity of pulse-based models comes from the encoding process that can be viewed as the continuous limit of data-reuploading in gate-based models. Subsequently, we prove that the pulse-based model can approximate arbitrary nonlinear functions when the underlying physical system is ensemble controllable. Under this condition, numerical simulations show that the expressivity can be enhanced by either increasing the pulse length or the number of qubits. As anticipated, we demonstrate through numerical examples that the pulse-based model can unleash more expressive power compared to the gate-based model. These findings establish a theoretical foundation for understanding and designing expressive QML models using NISQ devices.

On compression rate of quantum autoencoders: Control design, numerical and experimental realization

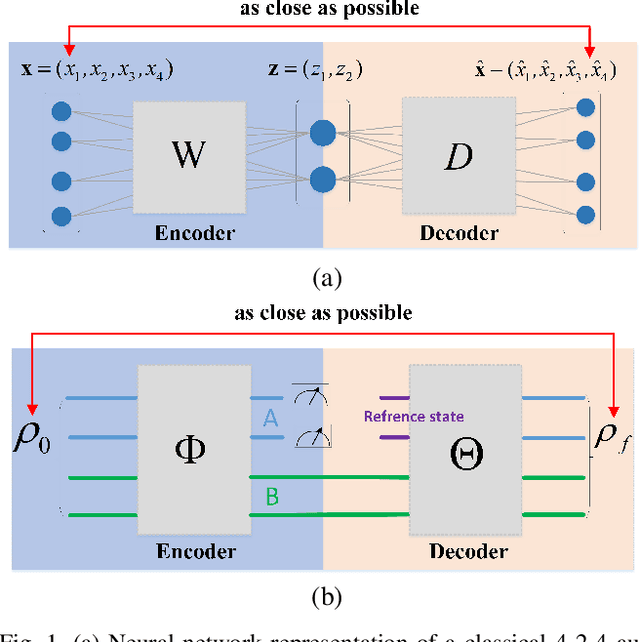
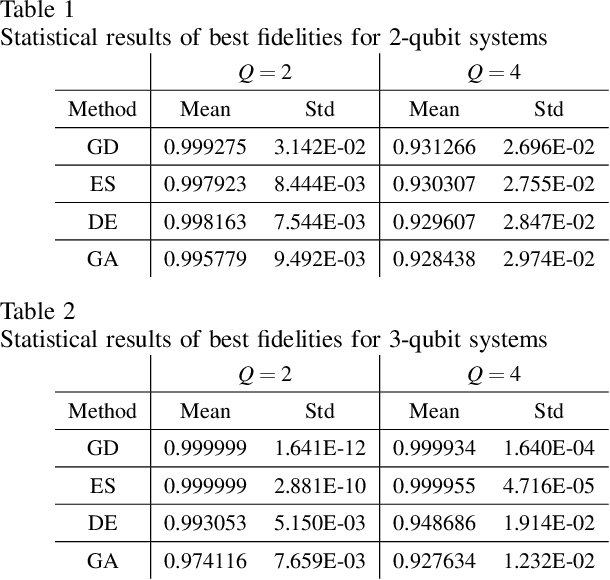
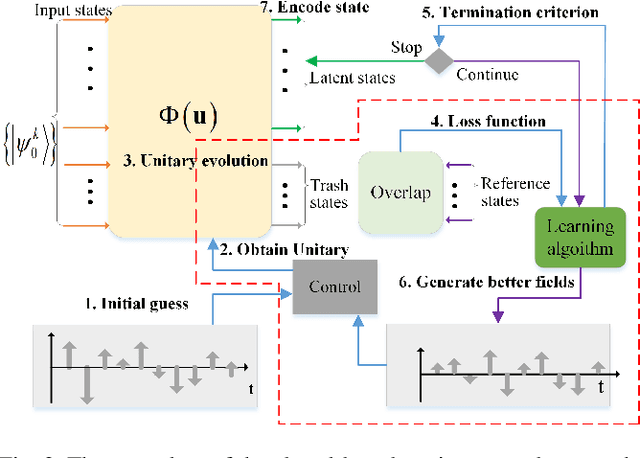
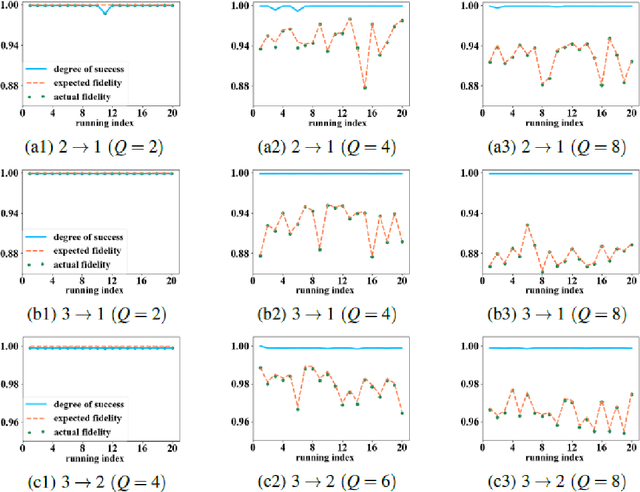
Quantum autoencoders which aim at compressing quantum information in a low-dimensional latent space lie in the heart of automatic data compression in the field of quantum information. In this paper, we establish an upper bound of the compression rate for a given quantum autoencoder and present a learning control approach for training the autoencoder to achieve the maximal compression rate. The upper bound of the compression rate is theoretically proven using eigen-decomposition and matrix differentiation, which is determined by the eigenvalues of the density matrix representation of the input states. Numerical results on 2-qubit and 3-qubit systems are presented to demonstrate how to train the quantum autoencoder to achieve the theoretically maximal compression, and the training performance using different machine learning algorithms is compared. Experimental results of a quantum autoencoder using quantum optical systems are illustrated for compressing two 2-qubit states into two 1-qubit states.