On compression rate of quantum autoencoders: Control design, numerical and experimental realization
Paper and Code
May 22, 2020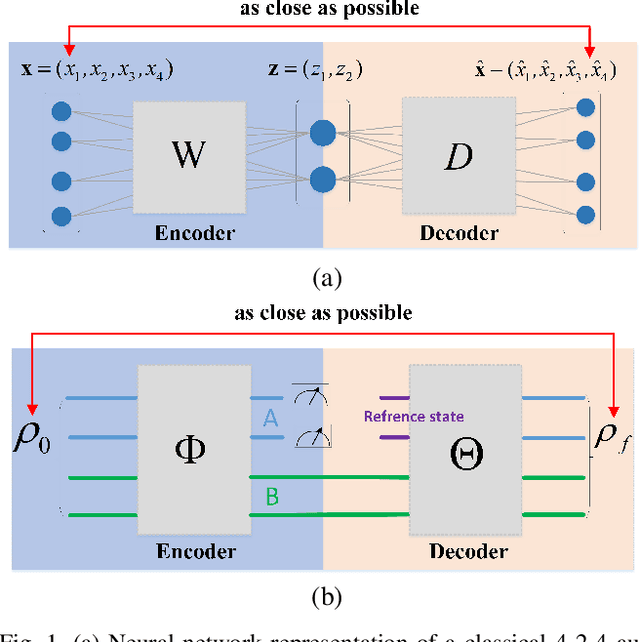
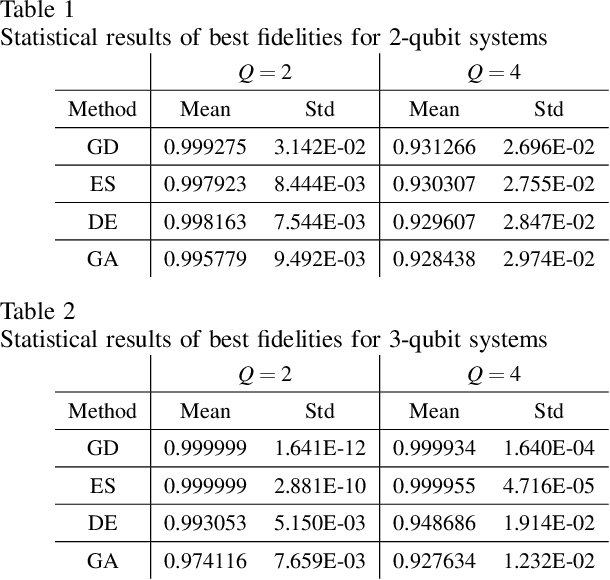
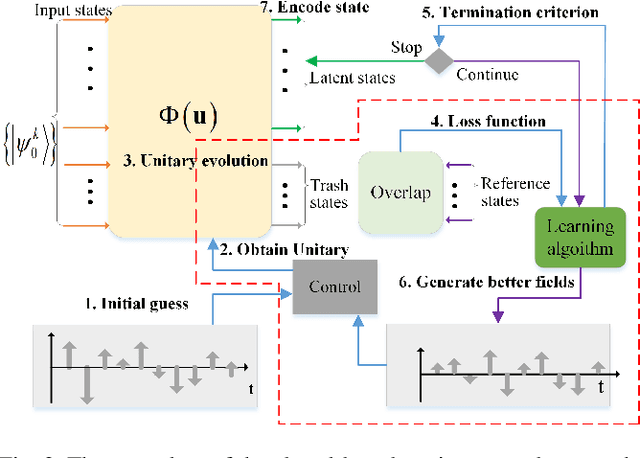
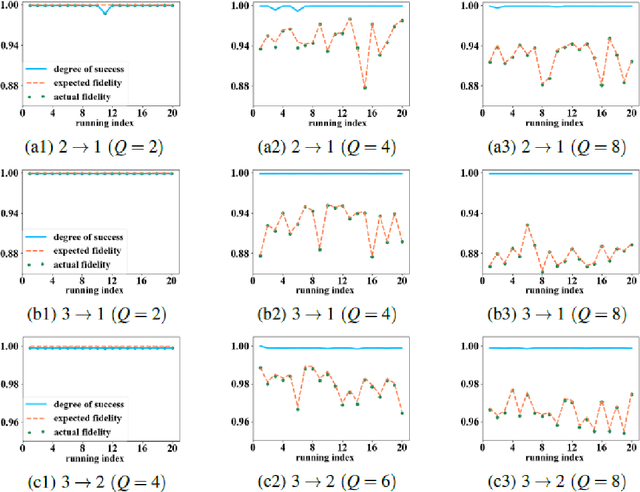
Quantum autoencoders which aim at compressing quantum information in a low-dimensional latent space lie in the heart of automatic data compression in the field of quantum information. In this paper, we establish an upper bound of the compression rate for a given quantum autoencoder and present a learning control approach for training the autoencoder to achieve the maximal compression rate. The upper bound of the compression rate is theoretically proven using eigen-decomposition and matrix differentiation, which is determined by the eigenvalues of the density matrix representation of the input states. Numerical results on 2-qubit and 3-qubit systems are presented to demonstrate how to train the quantum autoencoder to achieve the theoretically maximal compression, and the training performance using different machine learning algorithms is compared. Experimental results of a quantum autoencoder using quantum optical systems are illustrated for compressing two 2-qubit states into two 1-qubit states.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge