Greg Blekherman
Reconstruction of Backbone Curves for Snake Robots
Dec 09, 2020
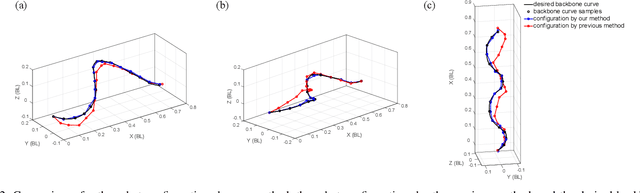
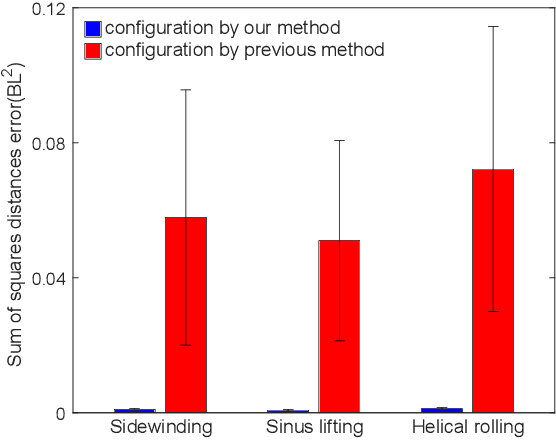

Abstract:Snake robots composed of alternating single-axis pitch and yaw joints have many internal degrees of freedom, which make them capable of versatile three-dimensional locomotion. Often, snake robot motions are planned kinematically by a chronological sequence of continuous backbone curves that capture desired macroscopic shapes of the robot. However, as the geometric arrangement of single-axis rotary joints creates constraints on the rotations in the robot, it is challenging for the robot to reconstruct an arbitrary 3-D curve. When the robot configuration does not accurately achieve the desired shapes defined by these backbone curves, the robot can have undesired contact with the environment, such that the robot does not achieve the desired motion. In this work, we propose a method for snake robots to reconstruct desired backbone curves by posing an optimization problem that exploits the robot's geometric structure. We verified that our method enables accurate curve-configuration conversions through its applications to commonly used 3-D gaits. We also demonstrated via robot experiments that 1) our method results in smooth locomotion on the robot; 2) our method allows the robot to approach the numerically predicted locomotive performance of a sequence of continuous backbone curve.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge