Confidence Interval Estimation of Predictive Performance in the Context of AutoML

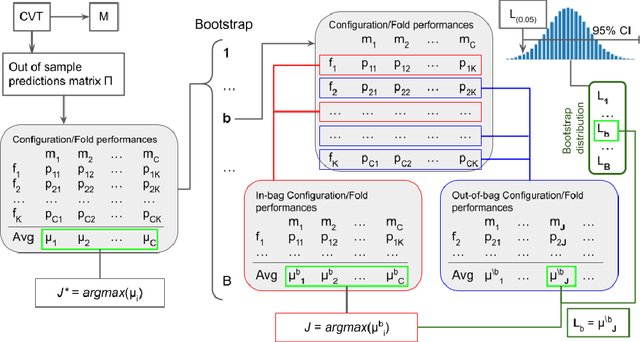
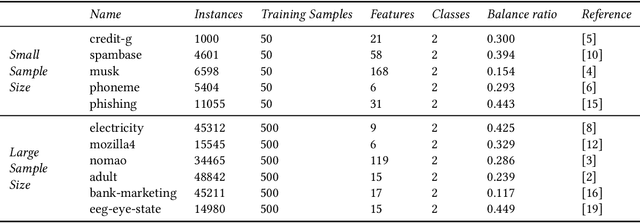
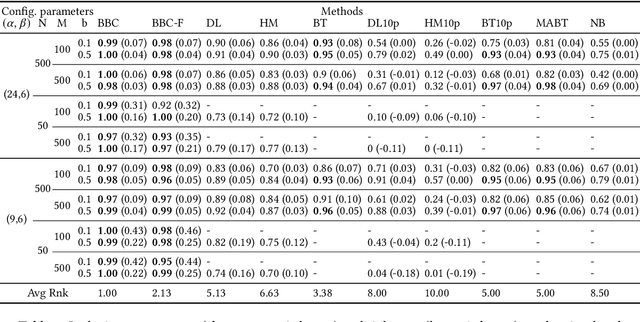
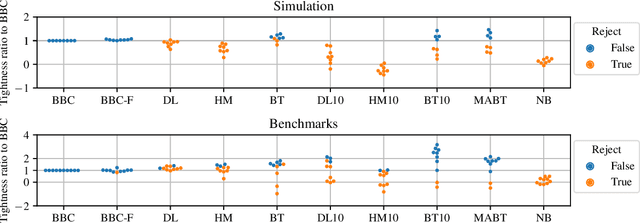
Any supervised machine learning analysis is required to provide an estimate of the out-of-sample predictive performance. However, it is imperative to also provide a quantification of the uncertainty of this performance in the form of a confidence or credible interval (CI) and not just a point estimate. In an AutoML setting, estimating the CI is challenging due to the ``winner's curse", i.e., the bias of estimation due to cross-validating several machine learning pipelines and selecting the winning one. In this work, we perform a comparative evaluation of 9 state-of-the-art methods and variants in CI estimation in an AutoML setting on a corpus of real and simulated datasets. The methods are compared in terms of inclusion percentage (does a 95\% CI include the true performance at least 95\% of the time), CI tightness (tighter CIs are preferable as being more informative), and execution time. The evaluation is the first one that covers most, if not all, such methods and extends previous work to imbalanced and small-sample tasks. In addition, we present a variant, called BBC-F, of an existing method (the Bootstrap Bias Correction, or BBC) that maintains the statistical properties of the BBC but is more computationally efficient. The results support that BBC-F and BBC dominate the other methods in all metrics measured.

A Meta-Level Learning Algorithm for Sequential Hyper-Parameter Space Reduction in AutoML

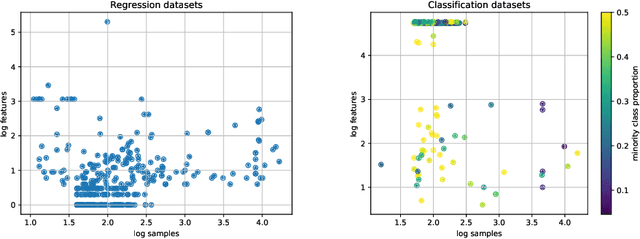
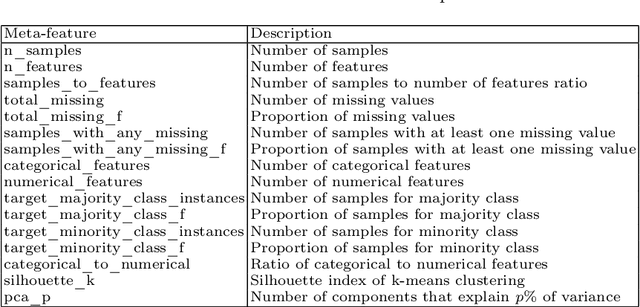
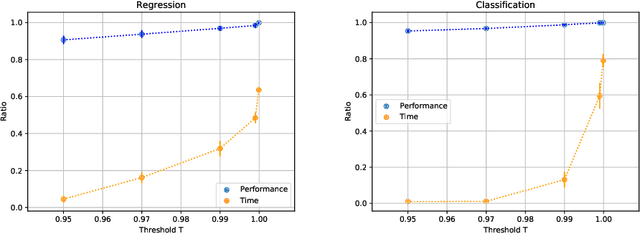
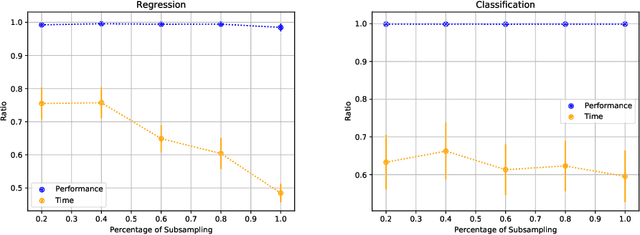
AutoML platforms have numerous options for the algorithms to try for each step of the analysis, i.e., different possible algorithms for imputation, transformations, feature selection, and modelling. Finding the optimal combination of algorithms and hyper-parameter values is computationally expensive, as the number of combinations to explore leads to an exponential explosion of the space. In this paper, we present the Sequential Hyper-parameter Space Reduction (SHSR) algorithm that reduces the space for an AutoML tool with negligible drop in its predictive performance. SHSR is a meta-level learning algorithm that analyzes past runs of an AutoML tool on several datasets and learns which hyper-parameter values to filter out from consideration on a new dataset to analyze. SHSR is evaluated on 284 classification and 375 regression problems, showing an approximate 30% reduction in execution time with a performance drop of less than 0.1%.

Bootstrapping the Out-of-sample Predictions for Efficient and Accurate Cross-Validation

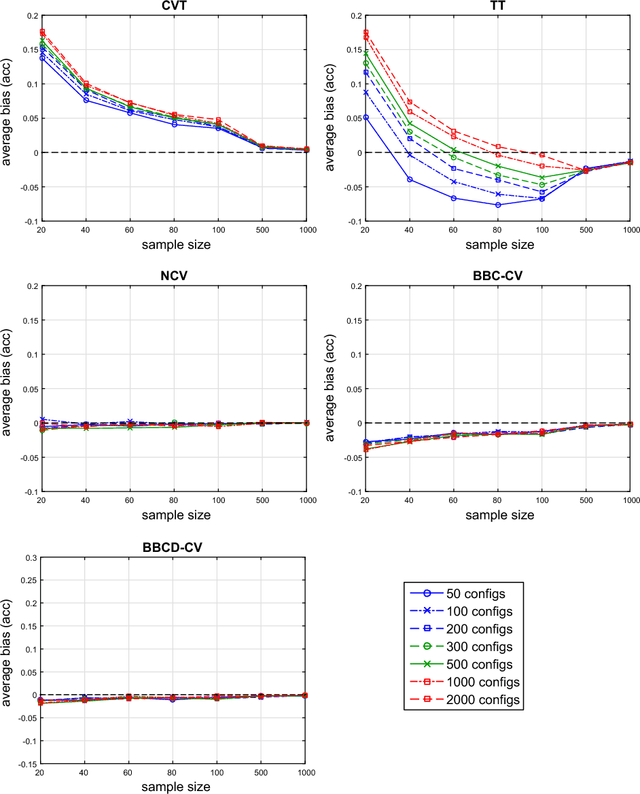
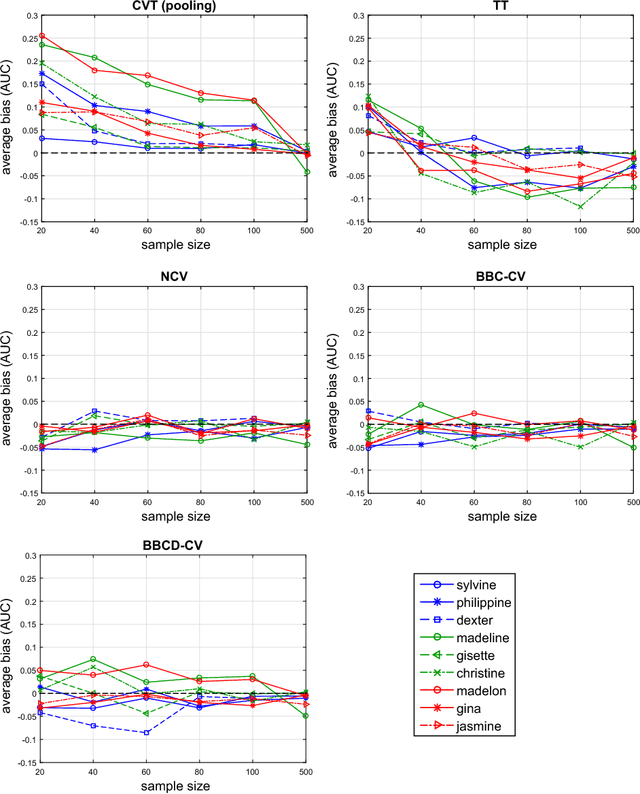
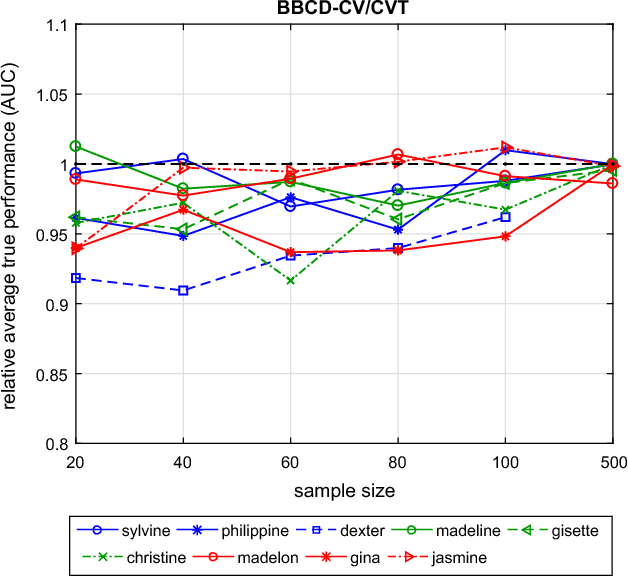
Cross-Validation (CV), and out-of-sample performance-estimation protocols in general, are often employed both for (a) selecting the optimal combination of algorithms and values of hyper-parameters (called a configuration) for producing the final predictive model, and (b) estimating the predictive performance of the final model. However, the cross-validated performance of the best configuration is optimistically biased. We present an efficient bootstrap method that corrects for the bias, called Bootstrap Bias Corrected CV (BBC-CV). BBC-CV's main idea is to bootstrap the whole process of selecting the best-performing configuration on the out-of-sample predictions of each configuration, without additional training of models. In comparison to the alternatives, namely the nested cross-validation and a method by Tibshirani and Tibshirani, BBC-CV is computationally more efficient, has smaller variance and bias, and is applicable to any metric of performance (accuracy, AUC, concordance index, mean squared error). Subsequently, we employ again the idea of bootstrapping the out-of-sample predictions to speed up the CV process. Specifically, using a bootstrap-based hypothesis test we stop training of models on new folds of statistically-significantly inferior configurations. We name the method Bootstrap Corrected with Early Dropping CV (BCED-CV) that is both efficient and provides accurate performance estimates.

Massively-Parallel Feature Selection for Big Data

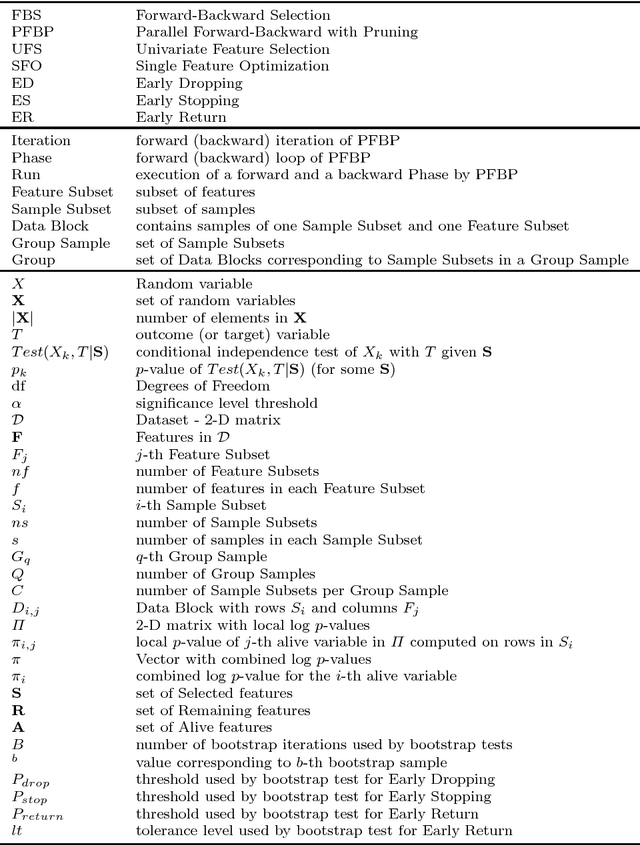
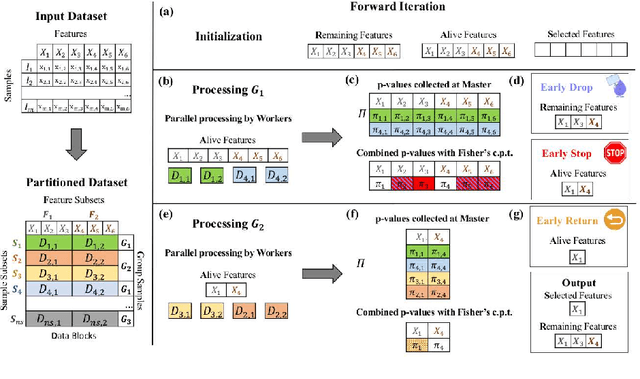
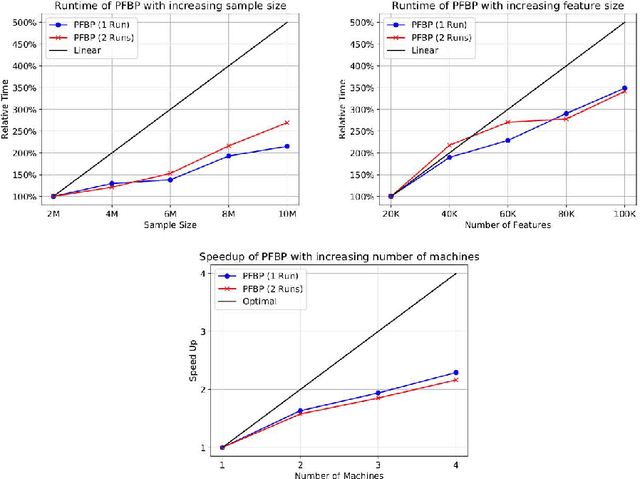
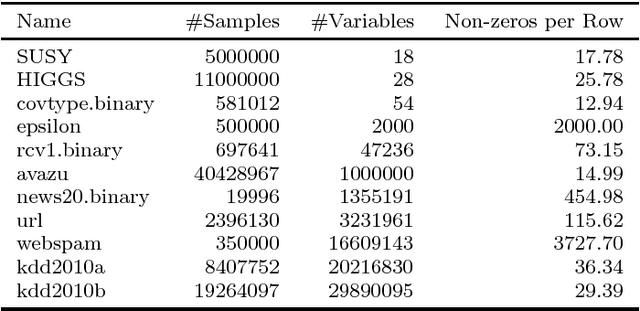
We present the Parallel, Forward-Backward with Pruning (PFBP) algorithm for feature selection (FS) in Big Data settings (high dimensionality and/or sample size). To tackle the challenges of Big Data FS PFBP partitions the data matrix both in terms of rows (samples, training examples) as well as columns (features). By employing the concepts of $p$-values of conditional independence tests and meta-analysis techniques PFBP manages to rely only on computations local to a partition while minimizing communication costs. Then, it employs powerful and safe (asymptotically sound) heuristics to make early, approximate decisions, such as Early Dropping of features from consideration in subsequent iterations, Early Stopping of consideration of features within the same iteration, or Early Return of the winner in each iteration. PFBP provides asymptotic guarantees of optimality for data distributions faithfully representable by a causal network (Bayesian network or maximal ancestral graph). Our empirical analysis confirms a super-linear speedup of the algorithm with increasing sample size, linear scalability with respect to the number of features and processing cores, while dominating other competitive algorithms in its class.

Forward-Backward Selection with Early Dropping

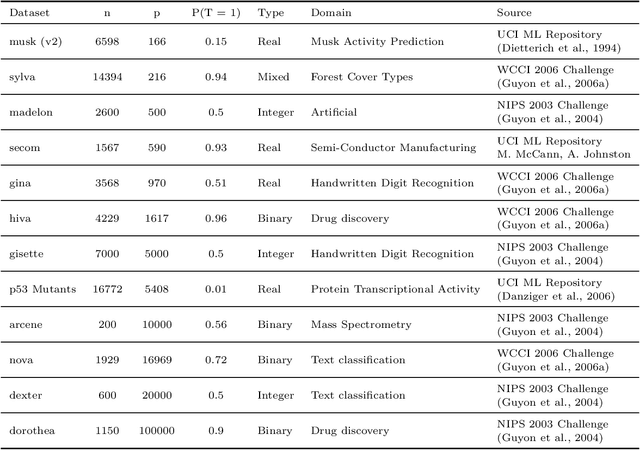
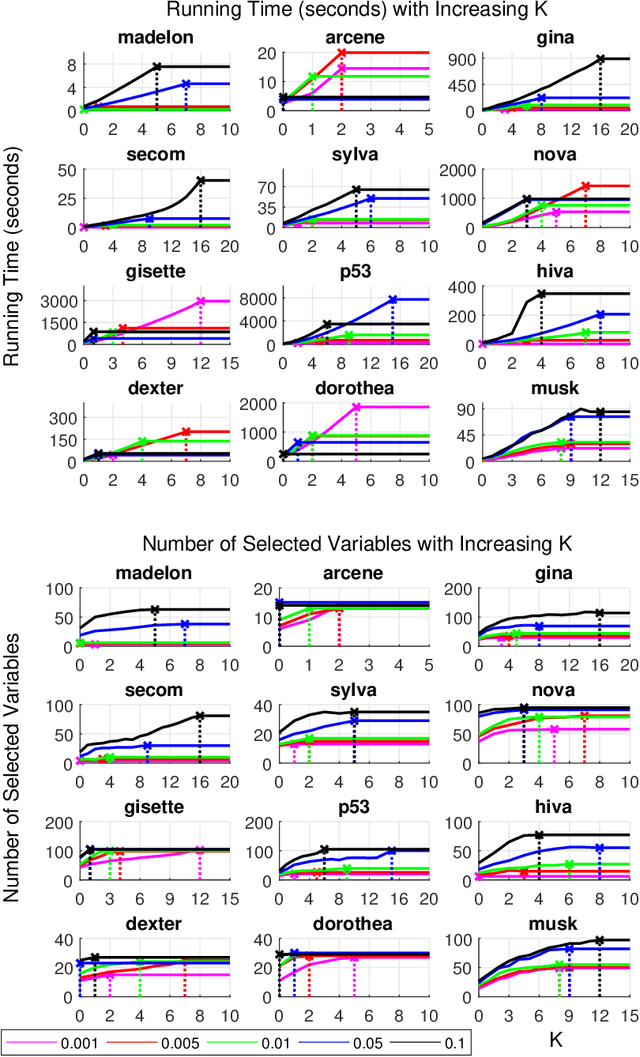
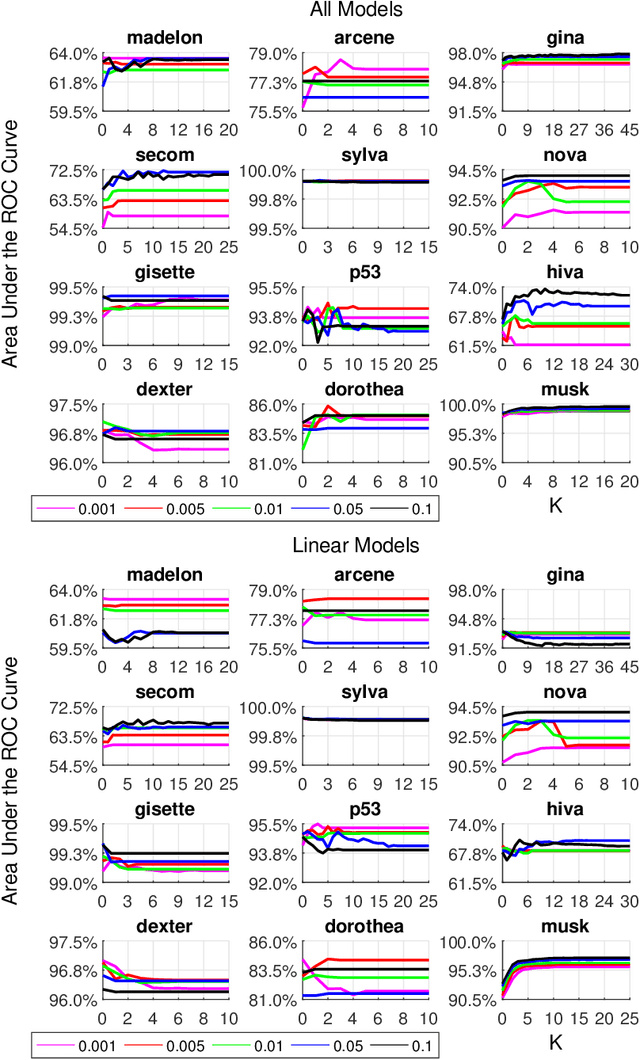
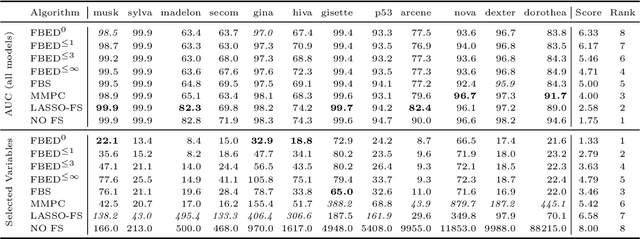
Forward-backward selection is one of the most basic and commonly-used feature selection algorithms available. It is also general and conceptually applicable to many different types of data. In this paper, we propose a heuristic that significantly improves its running time, while preserving predictive accuracy. The idea is to temporarily discard the variables that are conditionally independent with the outcome given the selected variable set. Depending on how those variables are reconsidered and reintroduced, this heuristic gives rise to a family of algorithms with increasingly stronger theoretical guarantees. In distributions that can be faithfully represented by Bayesian networks or maximal ancestral graphs, members of this algorithmic family are able to correctly identify the Markov blanket in the sample limit. In experiments we show that the proposed heuristic increases computational efficiency by about two orders of magnitude in high-dimensional problems, while selecting fewer variables and retaining predictive performance. Furthermore, we show that the proposed algorithm and feature selection with LASSO perform similarly when restricted to select the same number of variables, making the proposed algorithm an attractive alternative for problems where no (efficient) algorithm for LASSO exists.

Scoring and Searching over Bayesian Networks with Causal and Associative Priors

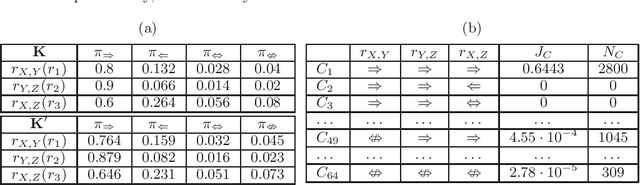
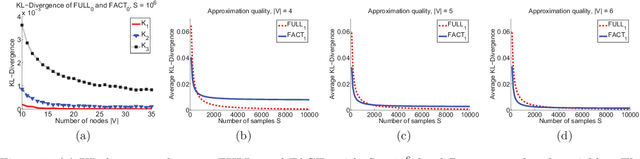
A significant theoretical advantage of search-and-score methods for learning Bayesian Networks is that they can accept informative prior beliefs for each possible network, thus complementing the data. In this paper, a method is presented for assigning priors based on beliefs on the presence or absence of certain paths in the true network. Such beliefs correspond to knowledge about the possible causal and associative relations between pairs of variables. This type of knowledge naturally arises from prior experimental and observational data, among others. In addition, a novel search-operator is proposed to take advantage of such prior knowledge. Experiments show that, using path beliefs improves the learning of the skeleton, as well as the edge directions in the network.

Incorporating Causal Prior Knowledge as Path-Constraints in Bayesian Networks and Maximal Ancestral Graphs

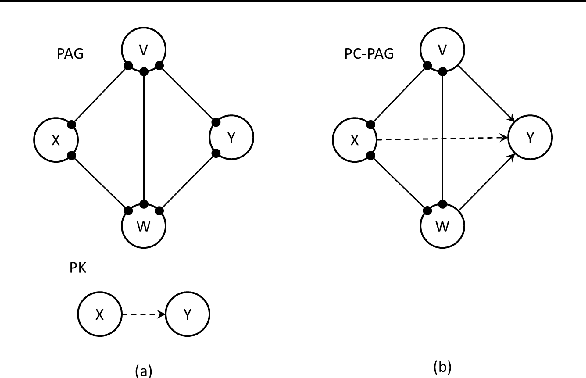
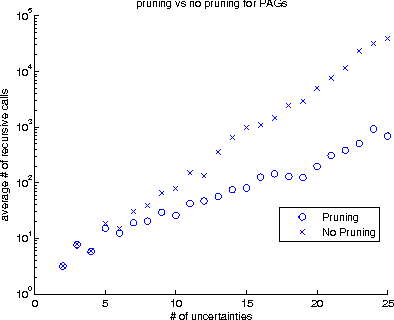
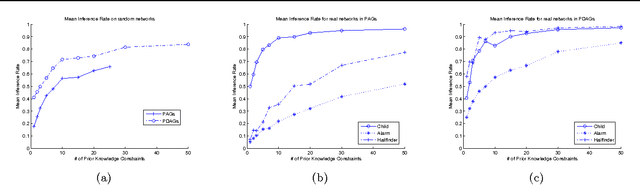
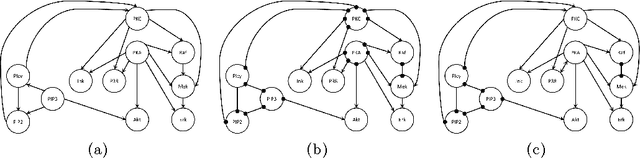
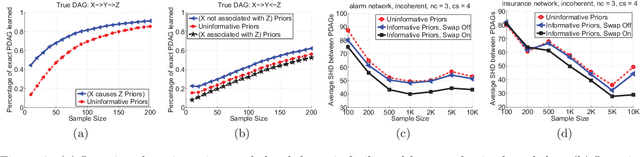
We consider the incorporation of causal knowledge about the presence or absence of (possibly indirect) causal relations into a causal model. Such causal relations correspond to directed paths in a causal model. This type of knowledge naturally arises from experimental data, among others. Specifically, we consider the formalisms of Causal Bayesian Networks and Maximal Ancestral Graphs and their Markov equivalence classes: Partially Directed Acyclic Graphs and Partially Oriented Ancestral Graphs. We introduce sound and complete procedures which are able to incorporate causal prior knowledge in such models. In simulated experiments, we show that often considering even a few causal facts leads to a significant number of new inferences. In a case study, we also show how to use real experimental data to infer causal knowledge and incorporate it into a real biological causal network. The code is available at mensxmachina.org.