Pavlos Katsogridakis
Massively-Parallel Feature Selection for Big Data
Aug 23, 2017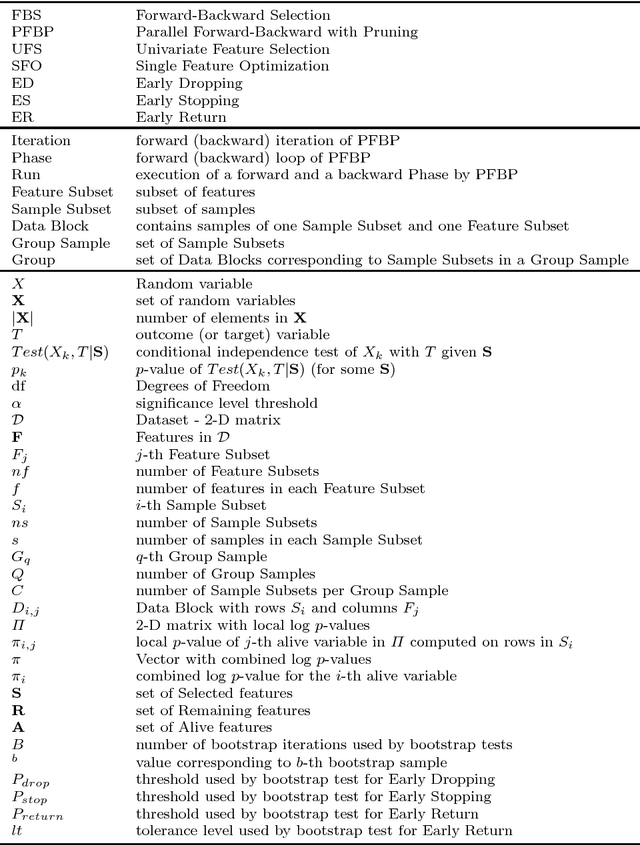
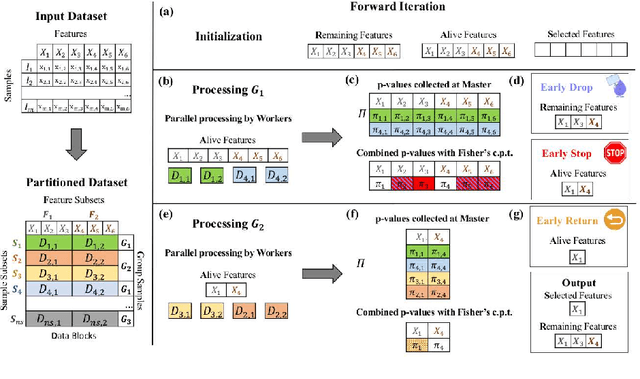
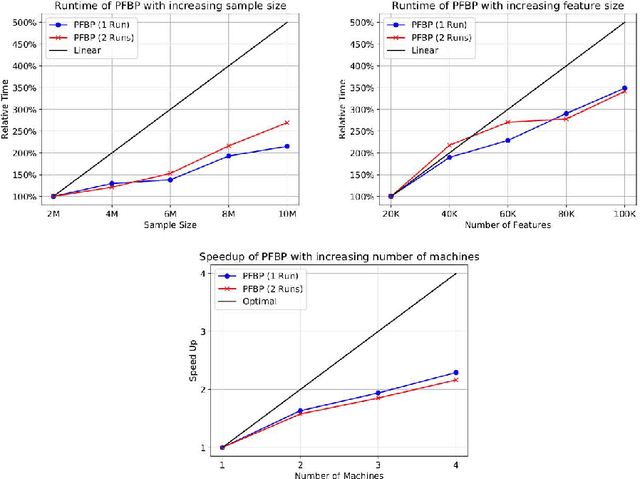
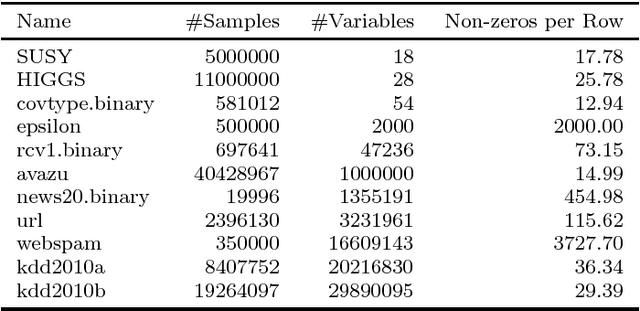
Abstract:We present the Parallel, Forward-Backward with Pruning (PFBP) algorithm for feature selection (FS) in Big Data settings (high dimensionality and/or sample size). To tackle the challenges of Big Data FS PFBP partitions the data matrix both in terms of rows (samples, training examples) as well as columns (features). By employing the concepts of $p$-values of conditional independence tests and meta-analysis techniques PFBP manages to rely only on computations local to a partition while minimizing communication costs. Then, it employs powerful and safe (asymptotically sound) heuristics to make early, approximate decisions, such as Early Dropping of features from consideration in subsequent iterations, Early Stopping of consideration of features within the same iteration, or Early Return of the winner in each iteration. PFBP provides asymptotic guarantees of optimality for data distributions faithfully representable by a causal network (Bayesian network or maximal ancestral graph). Our empirical analysis confirms a super-linear speedup of the algorithm with increasing sample size, linear scalability with respect to the number of features and processing cores, while dominating other competitive algorithms in its class.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge