Breaking hypothesis testing for failure rates

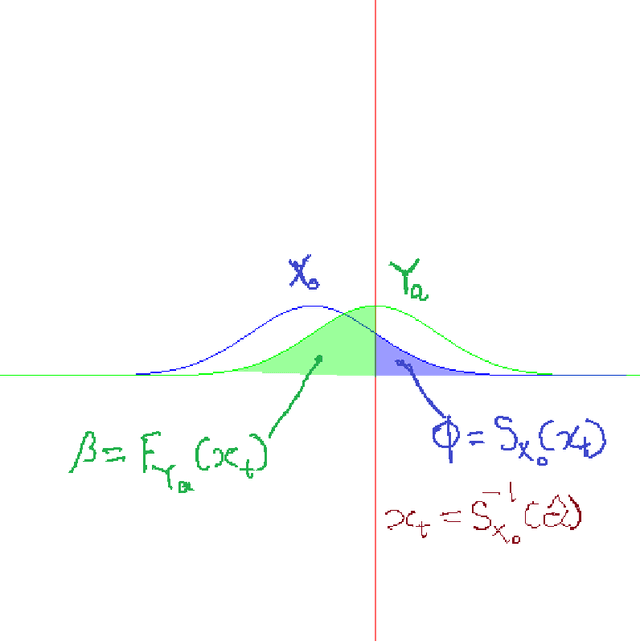
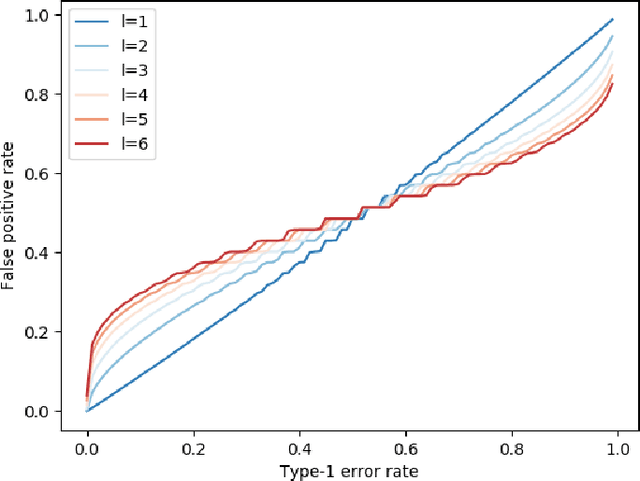
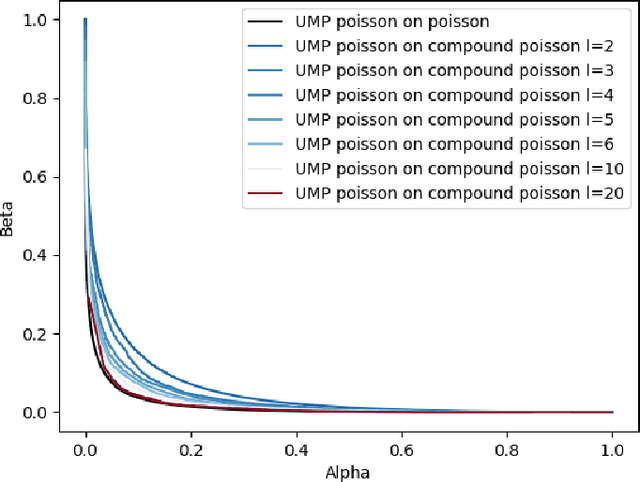
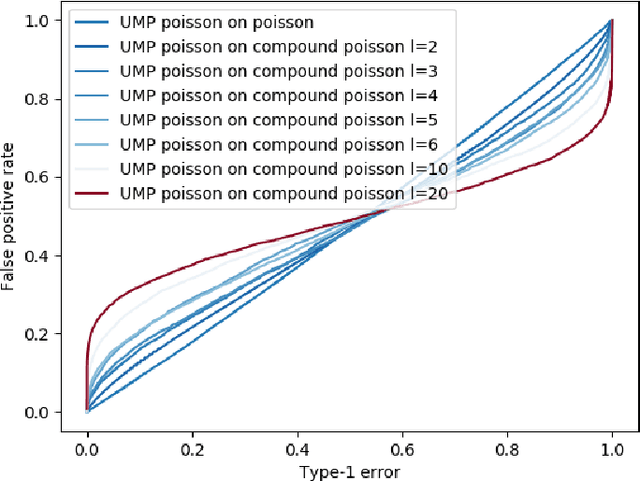
We describe the utility of point processes and failure rates and the most common point process for modeling failure rates, the Poisson point process. Next, we describe the uniformly most powerful test for comparing the rates of two Poisson point processes for a one-sided test (henceforth referred to as the "rate test"). A common argument against using this test is that real world data rarely follows the Poisson point process. We thus investigate what happens when the distributional assumptions of tests like these are violated and the test still applied. We find a non-pathological example (using the rate test on a Compound Poisson distribution with Binomial compounding) where violating the distributional assumptions of the rate test make it perform better (lower error rates). We also find that if we replace the distribution of the test statistic under the null hypothesis with any other arbitrary distribution, the performance of the test (described in terms of the false negative rate to false positive rate trade-off) remains exactly the same. Next, we compare the performance of the rate test to a version of the Wald test customized to the Negative Binomial point process and find it to perform very similarly while being much more general and versatile. Finally, we discuss the applications to Microsoft Azure. The code for all experiments performed is open source and linked in the introduction.

Optimizing Waiting Thresholds Within A State Machine

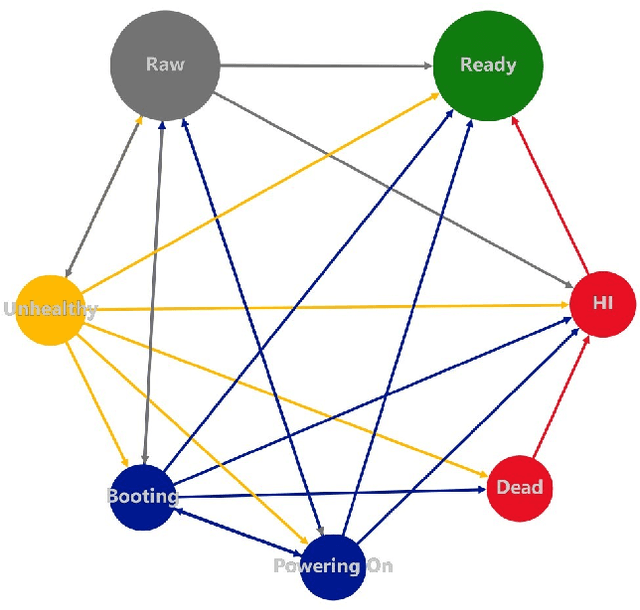
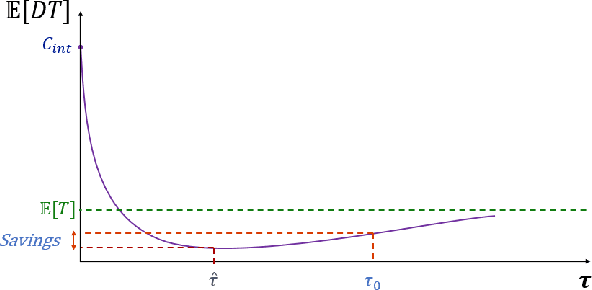
Azure (the cloud service provided by Microsoft) is composed of physical computing units which are called nodes. These nodes are controlled by a software component called Fabric Controller (FC), which can consider the nodes to be in one of many different states such as Ready, Unhealthy, Booting, etc. Some of these states correspond to a node being unresponsive to FCs requests. When a node goes unresponsive for more than a set threshold, FC intervenes and reboots the node. We minimized the downtime caused by the intervention threshold when a node switches to the Unhealthy state by fitting various heavy-tail probability distributions. We consider using features of the node to customize the organic recovery model to the individual nodes that go unhealthy. This regression approach allows us to use information about the node like hardware, software versions, historical performance indicators, etc. to inform the organic recovery model and hence the optimal threshold. In another direction, we consider generalizing this to an arbitrary number of thresholds within the node state machine (or Markov chain). When the states become intertwined in ways that different thresholds start affecting each other, we can't simply optimize each of them in isolation. For best results, we must consider this as an optimization problem in many variables (the number of thresholds). We no longer have a nice closed form solution for this more complex problem like we did with one threshold, but we can still use numerical techniques (gradient descent) to solve it.